题目内容
【题目】数列{an}中,定义:dn=an+2+an﹣2an+1(n≥1),a1=1.
(1)若dn=an , a2=2,求an;
(2)若a2=﹣2,dn≥1,求证此数列满足an≥﹣5(n∈N*);
(3)若|dn|=1,a2=1且数列{an}的周期为4,即an+4=an(n≥1),写出所有符合条件的{dn}.
【答案】
(1)解:∵an=dn=an+2+an﹣2an+1(n≥1),
∴an+2﹣2an+1=0(n≥1);
又∵a1=1,a2=2,
∴数列是以1为首项,2为公比的等比数列,
故数列{an}的通项公式为 ![]() ;
;
(2)解:证明:∵dn≥1,
∴an+2+an﹣2an+1≥1,
令cn=an+1﹣an,则
cn+1﹣cn≥1,
叠加得,cn≥n﹣4;
即an+1﹣an≥n﹣4,
叠加可得, ![]() ≥﹣5.
≥﹣5.
(3)解:由于|dn|=1,a1=1,a2=1,
若d1=1,则可得a3=2,
若d1=﹣1可得a3=0;
同理,若d2=1可得a4=4或a4=2,
若d2=﹣1可得a4=0或a4=﹣2;
具体如下表所示,
1,1, 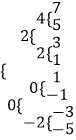 ;
;
所以{an}可以为1,1,2,2;1,1,2,2;1,1,2,2;…
或1,1,0,0;1,1,0,0;1,1,0,0;…
此时相应的{dn}为1,﹣1,﹣1,1,1,﹣1,﹣1,1,…
或﹣1,1,1,﹣1,﹣1,1,1,﹣1,….
【解析】(1)化简可得an+2﹣2an+1=0(n≥1);从而检验可得数列是以1为首项,2为公比的等比数列,从而求得;(2)由dn≥1,构造cn=an+1﹣an , 从而可得cn+1﹣cn≥1,从而可得an+1﹣an≥n﹣4,从而可得 ![]() ≥﹣5.(Ⅲ)由|dn|=1,a1=1,a2=1讨论求a3 , a4 , a5 , 从而归纳可得.
≥﹣5.(Ⅲ)由|dn|=1,a1=1,a2=1讨论求a3 , a4 , a5 , 从而归纳可得.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
