题目内容
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数 的单调区间,
的单调区间,
(2)若不等式 ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.
 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.(1)求实数a的值,并求函数
 的单调区间,
的单调区间,(2)若不等式
 ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.(1)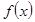 的单调递增区间是
的单调递增区间是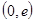 ,
,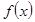 的单调递减区间是
的单调递减区间是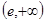 ;(2)
;(2)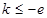 .
.
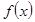 的单调递增区间是
的单调递增区间是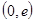 ,
,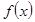 的单调递减区间是
的单调递减区间是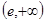 ;(2)
;(2)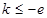 .
.试题分析:(1)先求
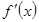 ,利用在
,利用在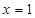 处的导数就是此点处切线斜率,即
处的导数就是此点处切线斜率,即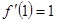 ,算出a,然后确定函数的定义域,利用
,算出a,然后确定函数的定义域,利用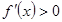 的区间为函数的增区间,
的区间为函数的增区间,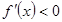 的区间为函数的减区间;(2)将不等式恒成立转化成
的区间为函数的减区间;(2)将不等式恒成立转化成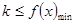 ,利用(1)
,利用(1)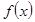 在
在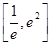 的单调性,判断出
的单调性,判断出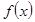 在
在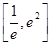 上的最小值为
上的最小值为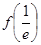 或
或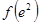 ,所以分别求出
,所以分别求出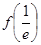 和
和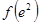 ,然后比较得出最小值.即
,然后比较得出最小值.即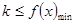 ,此题考察利用导数研究函数性质,逻辑推理要严谨,此题属于中档题.
,此题考察利用导数研究函数性质,逻辑推理要严谨,此题属于中档题.试题解析:(1)
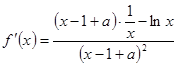
由题知:
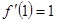 即
即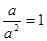 ,解得,
,解得, .
. ,定义域
,定义域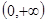
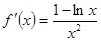 ,由
,由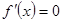 ,得
,得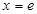 ,
,当
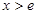 时,
时,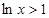 ,此时,
,此时,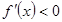 ,
,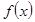 在
在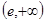 上单调递减.
上单调递减.当
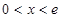 时,
时,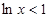 ,此时,
,此时,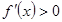 ,
,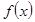 在
在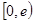 上单调递增.
上单调递增.综上:
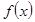 的单调递增区间是
的单调递增区间是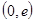 ,
,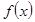 的单调递减区间是
的单调递减区间是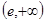 .
.(2)由(1)知
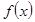 在上
在上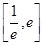 单调递增,在
单调递增,在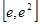 上单调递减.
上单调递减.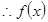 在
在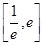 上的最小值为
上的最小值为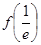 或
或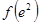
又
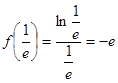 ,
,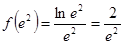 且
且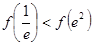
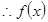 在
在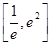 上的最小值为
上的最小值为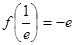
若
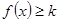 在
在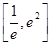 上恒成立,则
上恒成立,则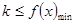
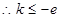

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的定义域为
的定义域为 ,且
,且 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 .
. ,
, ,判断
,判断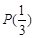 ,并说明理由;
,并说明理由; 若
若 的定义域为
的定义域为 ,
, 且
且 ,函数
,函数 .
. .
. 在
在 的单调性并用定义证明;
的单调性并用定义证明; ,求
,求 在区间
在区间 .
.
 的单调区间;
的单调区间; (
( )在
)在 上恒成立,求
上恒成立,求 的最大值.
的最大值.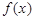 满足在集合
满足在集合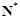 上的值域仍是集合
上的值域仍是集合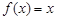 就是N函数.
就是N函数.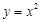 ,②
,②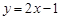 ,③
,③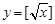 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);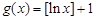 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;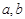 ,函数
,函数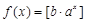 都不是N函数.
都不是N函数.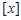 ”表示不超过
”表示不超过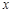 的最大整数)
的最大整数) 则m2+n2的取值范围是( )
则m2+n2的取值范围是( ) 的零点所在的区间是( ).
的零点所在的区间是( ). ,已知数列
,已知数列 满足:
满足:
 ,若对任意正整数
,若对任意正整数 ,都有
,都有
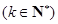 成立,则
成立,则 的值为( )
的值为( )



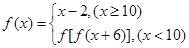 ,则
,则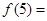 ( )
( )