题目内容
已知函数 .
.
(1)判断函数 在
在 的单调性并用定义证明;
的单调性并用定义证明;
(2)令 ,求
,求 在区间
在区间 的最大值的表达式
的最大值的表达式 .
.
 .
.(1)判断函数
 在
在 的单调性并用定义证明;
的单调性并用定义证明;(2)令
 ,求
,求 在区间
在区间 的最大值的表达式
的最大值的表达式 .
.(1)函数 在
在 递增;证明详见答案解析.
递增;证明详见答案解析.
(2)当 时,
时, ;当
;当 时,
时,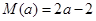 .
.
 在
在 递增;证明详见答案解析.
递增;证明详见答案解析. (2)当
 时,
时, ;当
;当 时,
时,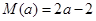 .
. 试题分析:(1)先根据已知条件求出
 ,再根据单调性的定义证明即可;
,再根据单调性的定义证明即可;(2)由(1)先求出
 的表达式,再根据单调性求得各个区间的最大值,综上即可求出
的表达式,再根据单调性求得各个区间的最大值,综上即可求出 在区间
在区间 的最大值的表达式
的最大值的表达式 .
.试题解析:(1)
 在
在 递增;
递增; 证明如下:
在区间
 上任取
上任取
则


而
 ,所以
,所以 ,
, >0
>0所以
 ,即函数
,即函数 在
在 的单调递增;(6分)
的单调递增;(6分)(2)若
 ,
, ,在
,在 递增,
递增, ,
,若
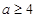 ,
, )在
)在 递减,
递减,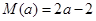 , (9分)
, (9分)若
 ,则
,则 (11分)
(11分)当
 时,函数递增,
时,函数递增, ,
,当
 时,函数递减,
时,函数递减, ; (13分)
; (13分) ,当
,当 时,
时, ,当
,当 时,
时,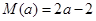 .
.综上:
 时,
时, ,当
,当 时,
时,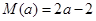 . (15分)
. (15分)
练习册系列答案
相关题目
 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1. 的单调区间,
的单调区间, 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.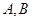 两城相距
两城相距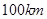 ,在两地之间距
,在两地之间距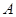 城
城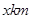 处
处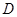 地建一核电站给
地建一核电站给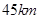 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(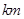 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数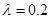 ,若
,若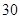 亿度/月,
亿度/月,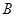 城为
城为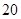 亿度/月.
亿度/月.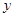 表示成
表示成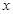 的函数,并求定义域;
的函数,并求定义域;

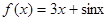 ,则满足不等式
,则满足不等式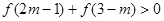 的m的取值范围为 .
的m的取值范围为 .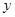 与时间
与时间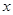 的关系,可选用( )
的关系,可选用( )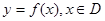 ,若存在常数
,若存在常数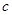 ,对任意
,对任意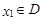 ,存在唯一
,存在唯一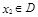 的,使得
的,使得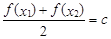 ,则称函数
,则称函数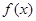 在
在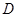 上的均值为
上的均值为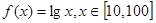 ,则函数
,则函数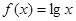 在
在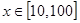 上的均值为。( )
上的均值为。( )



 ,则
,则 = .
= .