题目内容

设f(x)是定义在R上的增函数，且对于任意的x都有f(2－x)＋f(x)＝0成立．如果实数m，n满足不等式组则m2＋n2的取值范围是(　　)
A．(3，7)B．(9，25)C．(13，49)D．(9，49)
C
f(n2－8n)＝－f(2－n2＋8n)，故f(m2－6m＋23)＋f(n2－8n)<0，即f(m2－6m＋23)<f(2－n2＋8n)，由于函数f(x)是定义在R上的增函数，所以m2－6m＋23<2－n2＋8n，即(m－3)2＋(n－4)2<4，m>3，点(m，n)为平面上以(3，4)为圆心，2为半径的圆的右半部分的内部，故m2＋n2∈(13，49)．
练习册系列答案
相关题目
已知函数f(x)＝x2＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．
(1)证明：当x≥0时，f(x)≤(x＋c)2；
(2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c2－b2)恒成立，求M的最小值．
已知函数（a为常数）在x=1处的切线的斜率为1．
(1)求实数a的值，并求函数的单调区间，
(2)若不等式≥k在区间上恒成立，其中e为自然对数的底数，求实数k的取值范围．
某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图,当打出电话150分钟时,这两种方式电话费相差(　　)
A．10元B．20元C．30元D．元
若f(x)是奇函数，且x0是y＝f(x)＋ex的一个零点，则－x0一定是下列哪个函数的零点(　　)
A．y＝f(－x)ex－1 B．y＝f(x)e－x＋1
C．y＝exf(x)－1 D．y＝exf(x)＋1
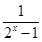若函数f(x)＝a－是定义在(－∞，－1]∪[1，＋∞)上的奇函数，则f(x)的值域为________．
设函数f(x)，g(x)的定义域分别为M，N，且M是N真子集，若对任意的x∈M，都有g(x)＝f(x)，则称g(x)是f(x)的“拓展函数”．已知函数f(x)＝log2x，若g(x)是f(x)的“拓展函数”，且g(x)是偶函数，则符合条件的一个g(x)的解析式是________．
函数f(x)＝x－sin x在区间[0,2π]上的零点个数为________．
．若直线与曲线恰有一个公共点，则实数的取值范围为       ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网