题目内容
若平面向量a=(1,x)和b=(2x+3,-x)互相平行,其中x∈R,
则|a-b|=( )
则|a-b|=( )
A.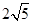 | B.2或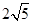 | C.-2或0 | D.2或10 |
B
试题分析:根据题意,由于平面向量a=(1,x)和b=(2x+3,-x),可知a-b=(-2x-2,2x),而根据两个向量是互相平行的,则可知所以1×(-x)-x×(2x+3)=0⇒x=0,或x=-2,
则可知a=(1,0)b=(3,0),或a=(1,-2)b=(-1,2),那么求解得到a-b=(-2,0),或a-b=(2,-4),结合模的定义可知答案为2或
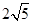 ,故选B.
,故选B.点评:此题考查了两向量平行的坐标表示法及方程思想求解未知量x的值,还考查了已知向量的坐标求向量的模.

练习册系列答案
相关题目
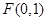 是中心在坐标原点
是中心在坐标原点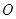 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆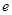 为
为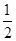 .
.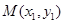 、
、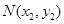 为椭圆
为椭圆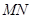 的斜率为
的斜率为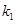 ;
;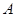 是满足
是满足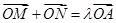 (
(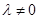 )的点,且直线
)的点,且直线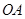 的斜率为
的斜率为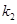 .
.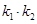 的值;
的值;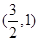 ,求实数
,求实数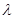 的取值范围.
的取值范围. 、
、 、
、 三点在一条直线上,
三点在一条直线上, ,
, ,
, ,且
,且 ,求实数
,求实数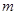 ,
, 的值.
的值. 、
、 、
、 且
且 满足
满足 ,则
,则 取得最小值时,点B的个数是( )
取得最小值时,点B的个数是( )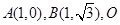 为坐标原点,点
为坐标原点,点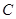 在第二象限,且
在第二象限,且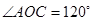 ,设
,设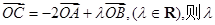 等于 ( )
等于 ( ) 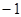
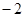
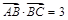 中,
中,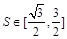 ,则
,则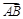 与
与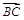 夹角的取值范围是_________.
夹角的取值范围是_________.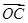 =
=
 +
+
 ,其中
,其中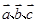 两两之间的夹角为60°,其模长都为1,则|
两两之间的夹角为60°,其模长都为1,则| 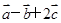 |等于
|等于 向量
向量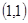 向上向左均平移1个单位后所得向量为 ;
向上向左均平移1个单位后所得向量为 ;