题目内容
空间直角坐标系中,O为坐标原点,已知两点坐标为A(3,1,0),B(-1,3,0),若点C满足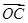 =
=
 +
+
 ,其中
,其中 ,
, ∈R,
∈R, +
+ =1,则点C的轨迹为
=1,则点C的轨迹为
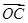 =
=
 +
+
 ,其中
,其中 ,
, ∈R,
∈R, +
+ =1,则点C的轨迹为
=1,则点C的轨迹为| A.平面 | B.直线 | C.圆 | D.线段 |
B
试题分析:设点C的坐标为(x,y,z ),由题意可得 (x,y,z )=(3
 -β,
-β, +3β,0 ),再由
+3β,0 ),再由 +
+ =1可得,x+2y-5=0,故点C的轨迹方程为 x+2y-5=0.解:设点C的坐标为(x,y,z ),由题意可得 (x,y,z )=(3
=1可得,x+2y-5=0,故点C的轨迹方程为 x+2y-5=0.解:设点C的坐标为(x,y,z ),由题意可得 (x,y,z )=(3 -
- ,
, +3
+3 ,0 )再由
,0 )再由 +
+ =1可得 x=3
=1可得 x=3 -
- =3-4
=3-4 ,y=
,y= +3
+3 =1+2β,故有 x+2y-5=0,故点C的轨迹方程为 x+2y-5=0,则点C的轨迹为直线,故选 B.
=1+2β,故有 x+2y-5=0,故点C的轨迹方程为 x+2y-5=0,则点C的轨迹为直线,故选 B.点评:本题考查点轨迹方程的求法,两个向量坐标形式的运算,求出x+2y-5=0,是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 ,
, ,
, ,若平面区域
,若平面区域 由所有满足
由所有满足 (
( ,
, )的点
)的点 组成,则
组成,则 中,设内角
中,设内角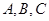 的对边分别为
的对边分别为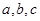 向量
向量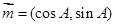 ,向量
,向量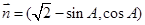 ,若
,若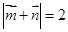
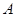 的大小 ;
的大小 ;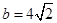 ,且
,且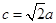 ,求
,求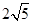
 ,
, ,若向量
,若向量 满足
满足 ,
, ,则
,则


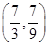
 所在的平面内有一点P,如果
所在的平面内有一点P,如果 ,那么
,那么 和面积与
和面积与



 ,
, ,若
,若 与
与 垂直,则
垂直,则 的值为 ( )
的值为 ( )



 =a,
=a, =b,
=b, =с,
=с, =d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
=d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形? 的三边长分别为
的三边长分别为 ,以点
,以点 为圆心,
为圆心, 为半径作一个圆.
为半径作一个圆. 为
为 的任意一条直径,记
的任意一条直径,记 ,求
,求 的最大值和最小值,并说明当
的最大值和最小值,并说明当