题目内容
已知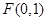 是中心在坐标原点
是中心在坐标原点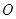 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 的离心率
的离心率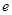 为
为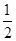 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设: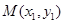 、
、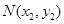 为椭圆
为椭圆 上不同的点,直线
上不同的点,直线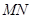 的斜率为
的斜率为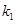 ;
;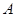 是满足
是满足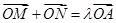 (
(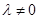 )的点,且直线
)的点,且直线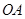 的斜率为
的斜率为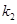 .
.
①求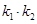 的值;
的值;
②若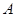 的坐标为
的坐标为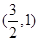 ,求实数
,求实数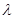 的取值范围.
的取值范围.
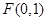 是中心在坐标原点
是中心在坐标原点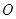 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 的离心率
的离心率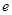 为
为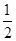 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设:
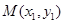 、
、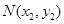 为椭圆
为椭圆 上不同的点,直线
上不同的点,直线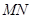 的斜率为
的斜率为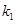 ;
;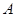 是满足
是满足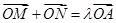 (
(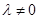 )的点,且直线
)的点,且直线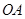 的斜率为
的斜率为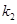 .
.①求
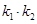 的值;
的值;②若
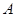 的坐标为
的坐标为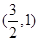 ,求实数
,求实数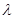 的取值范围.
的取值范围.(Ⅰ)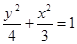 ;(Ⅱ)①
;(Ⅱ)①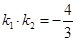 ;②实数
;②实数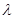 的取值范围是
的取值范围是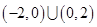 .
.
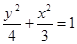 ;(Ⅱ)①
;(Ⅱ)①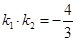 ;②实数
;②实数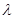 的取值范围是
的取值范围是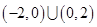 .
.试题分析:(Ⅰ)先根据题中的已知条件以及
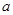 、
、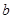 、
、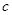 三者之间的关系求出
三者之间的关系求出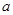 、
、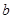 、
、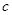 的值,从而确定椭圆
的值,从而确定椭圆 的方程;(Ⅱ)①解法一是利用斜率公式先将
的方程;(Ⅱ)①解法一是利用斜率公式先将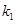 、
、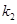 利用点
利用点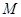 和
和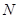 的坐标进行表示,然后借助点差法求出
的坐标进行表示,然后借助点差法求出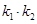 的值;解法二是将直线
的值;解法二是将直线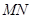 的方程假设出来,借助韦达定理与
的方程假设出来,借助韦达定理与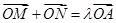 这一条件确定
这一条件确定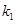 与
与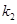 之间的关系,进而从相关等式中求出
之间的关系,进而从相关等式中求出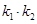 的值;②先确定直线
的值;②先确定直线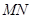 的斜率,然后假设直线
的斜率,然后假设直线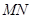 的方程为
的方程为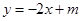 ,利用韦达定理确定
,利用韦达定理确定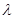 与
与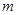 之间的等量关系,再利用直线
之间的等量关系,再利用直线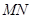 与椭圆
与椭圆 有两个不同的公共点结合
有两个不同的公共点结合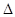 确定实数
确定实数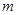 的取值范围,进而得到实数
的取值范围,进而得到实数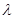 的取值范围.
的取值范围.试题解析:(Ⅰ)依题意,可设椭圆
 的方程为
的方程为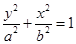 (
(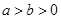 ), 1分
), 1分由
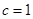 ,
,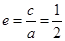 ,得
,得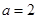 ,
,由
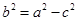 ,可得
,可得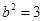 , 3分
, 3分故椭圆
 的方程为
的方程为 . 4分
. 4分(Ⅱ)解法一:①由
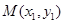 、
、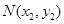 且
且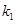 存在,得
存在,得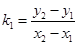 , 5分
, 5分由
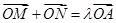 ,
,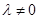 且
且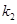 存在,得
存在,得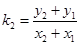 ,
,则
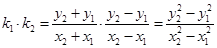 . 6分
. 6分∵
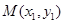 ,
,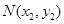 在椭圆上,∴
在椭圆上,∴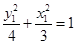 ,
,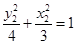 , 7分
, 7分两式相减得
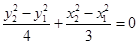 ,
,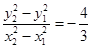 ,
,∴
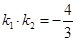 . 8分
. 8分②若
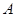 的坐标为
的坐标为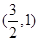 ,则
,则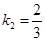 ,由①可得
,由①可得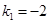 .
.设直线
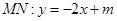 (
(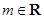 ),
),由
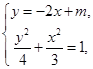 得
得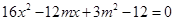 , 9分
, 9分所以
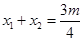 .
.∵
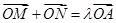 ,∴
,∴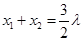 ,
,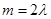 . 10分
. 10分又由
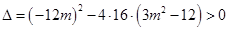 ,解得
,解得 , 11分
, 11分∴
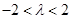 且
且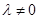 . 12分
. 12分解法二:①设直线
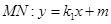 (
(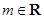 ),
),若
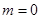 ,则
,则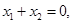
由
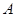 满足
满足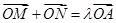 (
(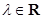 ,
,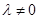 ),得
),得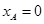 ,
,∵直线
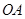 的斜率
的斜率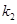 存在,∴
存在,∴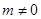 . 5分
. 5分由
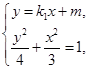 得
得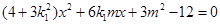 (*). 6分
(*). 6分∵
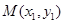 、
、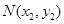 ,∴
,∴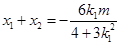 .
.  7分
7分∵
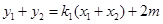 ,
,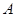 满足
满足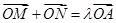 ,
,∴直线
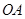 的斜率
的斜率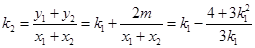 ,
,经化简得
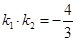 . 9分
. 9分②若
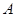 的坐标为
的坐标为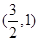 ,则
,则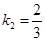 ,由①可得
,由①可得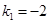 . 10分
. 10分∴方程(*)可化为
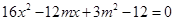 ,
,下同解法一.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
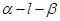 大小为
大小为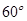 ,半平面
,半平面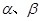 内分别有点A、B,
内分别有点A、B,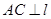 于C、
于C、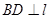 于D,已知AC=4、CD=5,DB=6,求线段AB的长.
于D,已知AC=4、CD=5,DB=6,求线段AB的长.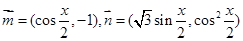 ,设函数
,设函数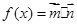
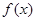 在区间
在区间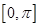 上的零点;
上的零点;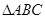 中,角
中,角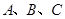 的对边分别是
的对边分别是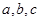 ,且满足
,且满足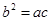 ,求
,求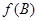 的取值范围.
的取值范围.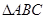 中,
中,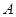 、
、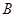 、
、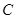 所对的边分别为
所对的边分别为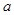 、
、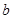 、
、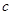 .已知向量
.已知向量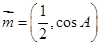 ,
,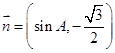 ,且
,且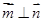 .
.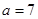 ,
,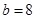 ,求
,求 中,
中,  ,
, ,
, ,则
,则
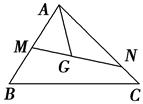
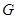 是
是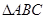 的重心,过
的重心,过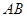 ,
,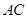 两边分别交于
两边分别交于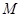 ,
,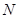 两点,且
两点,且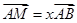 ,
,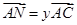 ,则
,则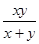 的值为( )
的值为( )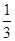
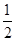
 ,
,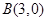 ,
, ,若平面区域
,若平面区域 由所有满足
由所有满足 (
( ,
, )的点
)的点 组成,则
组成,则 为平面的一组基向量,
为平面的一组基向量, ,
, ,
, 与
与 交与点
交与点

 关于
关于 ,
, ,求
,求 ;
; 交直线
交直线 于
于 两点,设
两点,设
 ,
, )求
)求 的关系式。
的关系式。