题目内容
20.己知函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$(x∈R).(1)求f(x)+f(1-x);
(2)求f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+…+f($\frac{2013}{2015}$)+f($\frac{2014}{2015}$)的值.
分析 (1)直接利用函数的解析式,可证f(x)+f(1-x)=1.
(2)由倒序相加法可得所求为1007对的组合,即1007个1,可得答案.
解答 解:(1)∵函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,
∴f(x)+f(1-x)=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{{4}^{1-x}}{{4}^{1-x}+2}$=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{{4}^{1-x}•{4}^{x}}{{{4}^{x}•{4}^{1-x}}^{\;}+2•{4}^{x}}$=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{2}{{4}^{x}+2}$=1.
f(x)+f(1-x)=1;
(2)由(1)可得S=f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+…+f($\frac{2013}{2015}$)+f($\frac{2014}{2015}$)=1007×1=1007.
点评 本题考查函数与方程的应用,倒序相加法求和,得出f(x)+f(1-x)=1并得出所求即为1007对项的和是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某办公室有男职工5人,女职工4人,欲从中抽调3人支援其他工作,但至少要有2位是男士,则抽凋方案有( )种.
| A. | 18 | B. | 30 | C. | 40 | D. | 50 |
9.已知log32=a,3b=5,则log3$\sqrt{30}$由a、b表示为( )
| A. | $\frac{1}{2}$(a+b+1) | B. | $\frac{1}{2}$(a+b)+1 | C. | $\frac{1}{3}$(a+b+1) | D. | $\frac{1}{2}$a+b+1 |
20.已知α,β为锐角三角形的两个锐角,则以下结论正确的是( )
| A. | sinα<sinβ | B. | cosα<sinβ | C. | cosα<cosβ | D. | cosα>cosβ |
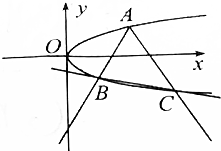 如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.
如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.