题目内容
5.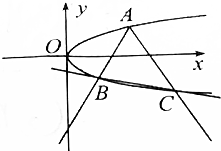 如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.
如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.
分析 设出直线BA、AC的方程与椭圆方程联立,求出C,B的坐标,利用斜率公式,即可证明直线BC的斜率为定值
解答 证明:∵点A坐标为(4,2),设B(x1,y1),C(x2,y2),
由已知设BA:m(y-2)=x-4,即:x=my-2m+4,
代入抛物线的方程得:y2=my-2m+4,即y2-my+2m-4=0,
则:y1+2=m,故:y1=m-2,
设CA:-m(y-2)=x-4,即:x=-my+2m+4,
代入抛物线的方程得:y2=-my+2m+4,即y2+my-2m-4=0,
则:y2+2=-m,故y2=-m-2,…(10分)
直线CB的斜率kCB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2m}{-8m}$=-$\frac{1}{4}$,
所以:直线BC的斜率为定值.
点评 本题考查的知识点是抛物线的性质,考查直线的斜率公式,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
相关题目
10.设lg2=a,则log225=( )
| A. | $\frac{1-a}{a}$ | B. | $\frac{a}{1-a}$ | C. | $\frac{2(1-a)}{a}$ | D. | $\frac{2a}{1-a}$ |
17.如果1gm=b-1gn,那么m等于( )
| A. | $\frac{b}{n}$ | B. | 10bn | C. | 10b+b | D. | $\frac{1{0}^{b}}{n}$ |
 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为$\frac{4}{3}$.
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为$\frac{4}{3}$.