题目内容
5．已知i为虚数单位，复数z满足1-i=$\frac{i}{z}$，则z的共轭复数等于（ ）| A． | 1-i | B． | 1+i | C． | $\frac{1}{2}$+$\frac{1}{2}$i | D． | -$\frac{1}{2}$-$\frac{1}{2}$i |
分析 通过求出复数z的表达式即得结论．
解答 解：∵1-i=$\frac{i}{z}$，∴z=$\frac{i}{1-i}$=$\frac{i（1+i）}{（1-i）（1+i）}$=$\frac{-1+i}{2}$，
∴z的共轭复数：$\overline{z}$=$\frac{-1-i}{2}$，
故选：D．
点评 本题考查复数的相关知识，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
15．
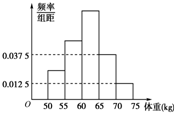为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（ ）
为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（ ）| A． | 6 | B． | 12 | C． | 18 | D． | 24 |
16．二次函数y=kx2（x＞0）的图象在点（an，an2）处的切线与x轴交点的横坐标为an+1，n为正整数，a1=$\frac{1}{3}$，若数列{an}的前n项和为Sn，则S5=（ ）
| A． | $\frac{3}{2}[{1-{{（{\frac{1}{3}}）}^5}}]$ | B． | $\frac{1}{3}[{1-{{（{\frac{1}{3}}）}^5}}]$ | C． | $\frac{2}{3}[{1-{{（{\frac{1}{2}}）}^5}}]$ | D． | $\frac{3}{2}[{1-{{（{\frac{1}{2}}）}^5}}]$ |
如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=2$\sqrt{2}$，PA=2，$\overrightarrow{PE}$=2$\overrightarrow{EC}$．
10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{6}$=1与抛物线y2=2px有公共焦点F，双曲线与抛物线的准线交于M、N两点，且△MNF为等边三角形，则p的值为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4$\sqrt{2}$ | D． | 6 |
