题目内容
20.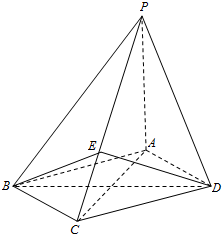 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2$\sqrt{2}$,PA=2,$\overrightarrow{PE}$=2$\overrightarrow{EC}$.
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2$\sqrt{2}$,PA=2,$\overrightarrow{PE}$=2$\overrightarrow{EC}$.(Ⅰ)证明:PC⊥平面BED;
(Ⅱ)若直线PD与平面PBC所成角为$\frac{π}{6}$,求二面角A-PB-C的大小.
分析 (I)先由已知建立空间直角坐标系,利用向量法即可证明;
(II)求出两个平面的法向量,利用空间向量夹角公式即可求得线面角的正弦值,进而求得线面角.
解答 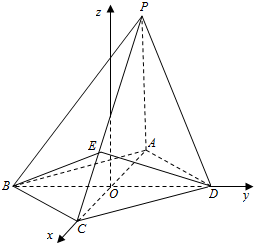 证明:(Ⅰ)设AC∩BD=0,以O为原点,OC为x轴,OD为y轴,建立空间直角坐标系如图:
证明:(Ⅰ)设AC∩BD=0,以O为原点,OC为x轴,OD为y轴,建立空间直角坐标系如图:
则A(-$\sqrt{2}$,0,0),C($\sqrt{2}$,0,0),P(-$\sqrt{2}$,0,2),
设B(0,-a,0),D(0,a,0),
由$\overrightarrow{PE}$=2$\overrightarrow{EC}$得E($\frac{\sqrt{2}}{3}$,0,$\frac{2}{3}$),
则$\overrightarrow{PC}$=(2$\sqrt{2}$,0,-2),$\overrightarrow{BE}$=($\frac{\sqrt{2}}{3}$,a,$\frac{2}{3}$),
$\overrightarrow{BD}$=(0,2a,0),
∴$\overrightarrow{PC}$•$\overrightarrow{BD}$=0,$\overrightarrow{PC}$•$\overrightarrow{BE}$=0,
∴$\overrightarrow{PC}$⊥$\overrightarrow{BD}$,$\overrightarrow{PC}$⊥$\overrightarrow{BE}$,
即PC⊥平面BED;
(Ⅱ)设平面PAB的法向量为$\overrightarrow{n}$=(x,y,z),
∵$\overrightarrow{AP}$=(0,0,2),$\overrightarrow{AB}$=($\sqrt{2}$,-a,0),
由$\overrightarrow{n}•\overrightarrow{AP}=0$,$\overrightarrow{n}•\overrightarrow{AB}=0$,解得$\overrightarrow{n}$=(1,$\frac{\sqrt{2}}{a}$,0),
设平面PBC的法向量为$\overrightarrow{m}$=(x,y,z),
$\overrightarrow{BC}$=($\sqrt{2}$,a,0),$\overrightarrow{CP}$=(-2$\sqrt{2}$,0,2),
由$\overrightarrow{m}$•$\overrightarrow{BC}$=0,$\overrightarrow{m}$•$\overrightarrow{CP}$=0,得$\overrightarrow{m}$=(1,-$\frac{\sqrt{2}}{a}$,$\sqrt{2}$),
∵直线PD与平面PBC所成角为$\frac{π}{6}$,
∴sin$\frac{π}{6}$=$\frac{|\overrightarrow{PD}•\overrightarrow{m}|}{|\overrightarrow{PD}•\overrightarrow{m}|}=\frac{1}{2}$,解得a=$\sqrt{2}$,
于是$\overrightarrow{m}•\overrightarrow{n}=1-\frac{2}{{a}^{2}}=0$,
即$\overrightarrow{m}⊥\overrightarrow{n}$,
则平面APB⊥平面PBC;
即二面角A-PB-C的大小为$\frac{π}{2}$.
点评 本题主要考查用空间向量求直线与平面的夹角;直线与平面垂直的判定;向量语言表述线面的垂直、平行关系.

| A. | 1-i | B. | 1+i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |