题目内容
若当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,则函数y=loga|
|的图象大致为( )
| 1 |
| x |
A、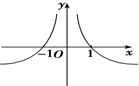 |
B、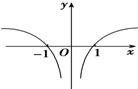 |
C、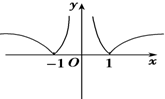 |
D、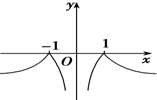 |
考点:函数的图象
专题:函数的性质及应用
分析:由于当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,利用指数函数的图象和性质可得0<a<1.先画出函数y=loga|x|的图象,此函数是偶函数,当x>0时,即为y=logax,而函数y=loga|
|=-loga|x|,即可得出图象.
| 1 |
| x |
解答:
解:∵当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1.
因此,必有0<a<1.
先画出函数y=loga|x|的图象:黑颜色的图象.
而函数y=loga|
|=-loga|x|,其图象如红颜色的图象.
故选B.

因此,必有0<a<1.
先画出函数y=loga|x|的图象:黑颜色的图象.
而函数y=loga|
| 1 |
| x |
故选B.
点评:本题考查指数函数与对数函数的图象及性质,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程
-x=
+1去分母得( )
| 2x+3 |
| 2 |
| 9x-5 |
| 3 |
| A、3(2x+3)-x=2(9x-5)+6 |
| B、3(2x+3)-6x=2(9x-5)+1 |
| C、3(2x+3)-x=2(9x-5)+1 |
| D、3(2x+3)-6x=2(9x-5)+6 |
复数
的共轭复数等于( )
| 1 |
| (1+i)2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|