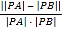题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
【答案】(1)证明见解析;(2)1
【解析】
(1)取AD的中点O, 连接P0,BO,BD,利用三线合一得出BO⊥AD,PO⊥AD,故AD⊥平面PBO,,于是AD⊥PB。(2)利用勾股定理得出PO⊥BO,可得PO⊥平面ABCD,用棱锥的体积公式计算即可
(1)证明:取AD的中点O,连接P0,BO,BD,
∵底面ABCD是等边三角形
∴BO⊥AD,
又∵PA=PD,即ΔPAD等腰三角形,
∴PO⊥AD,
又∵PO![]() BO=0.
BO=0.
∴AD⊥平面PBO,
又∵PB![]() 平面PBO.
平面PBO.
∴AD⊥PB;
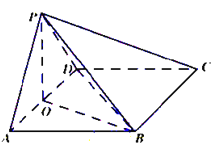
(2)解:AB=PA=2
∴由(1)知ΔPAD是边长为2的正三角形,则PO=![]() .
.
又∵PB=![]() ,
,
∴PO2+BO2=PB2,即PO⊥BO,
又由(1)知,PO⊥AD.且BO![]() AD=O.
AD=O.
∴PO⊥平面ABCD.
∴![]()
∴三棱锥P-BCD的体积为1.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()