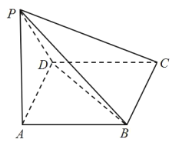
题目内容
【题目】(
已知函数![]() ,(
,(![]() )
)
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)设函数![]() 在区间
在区间![]() 内是减函数,求
内是减函数,求![]() 的取值范围.
的取值范围.
【答案】解:(1)![]()
![]() …………………………………………………………………1分
…………………………………………………………………1分
当![]() 时,即
时,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 上递增;…………………………………………………3分
上递增;…………………………………………………3分
当![]() 时,即
时,即![]() 或
或![]() 时,
时,![]() ,
,
由![]() 求得两根为
求得两根为![]() …………………………………5分
…………………………………5分
即![]() 在
在![]() 和
和![]() 上递增;
上递增;
在![]() 上递减,………………………………6分
上递减,………………………………6分
![]()
![]() 的单调递增区间是:当
的单调递增区间是:当![]() 时,
时,![]()
当![]() 或
或![]() 时,
时,![]() 和
和![]()
![]() 的单调递减区间是:
的单调递减区间是:
当![]() 或
或![]() 时,
时,![]() ………………7分
………………7分
(2)(法一)由(1)知![]() 在区间
在区间![]() 上递减,
上递减,
∴只要![]()
![]()
∴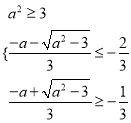 解得:
解得:![]() .
.
 ………9分
………9分
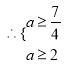 ……………………………………………………………12分
……………………………………………………………12分
![]()
![]() ……………………………………………………14分
……………………………………………………14分
【解析】
(1)![]() ;(2)
;(2)![]()
(1)![]() 求导:
求导:![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上递增
上递增
当![]() ,
,![]() 求得两根为
求得两根为![]()
即![]() 在
在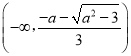 递增,
递增,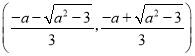 递减,
递减,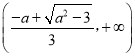 递增
递增
(2)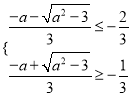 ,且
,且![]() 解得:
解得:![]()

 天天练口算系列答案
天天练口算系列答案【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
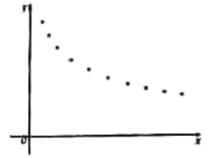
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适合作价格
哪一个更适合作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() ,求该产品投放市场第几天的销售额最高?最高为多少元?
,求该产品投放市场第几天的销售额最高?最高为多少元?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为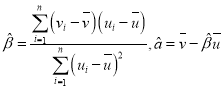 .
.