Question

【题目】设函数图象上不同两点，处的切线的斜率分别是，，规定（为线段的长度）叫做曲线在点与点之间的“弯曲度”，给出以下命题：

①函数图象上两点与的横坐标分别为和，则；

②存在这样的函数，其图象上任意不同两点之间的“弯曲度”为常数；

③设,是抛物线上不同的两点，则 ；

④设, 是曲线（是自然对数的底数）上不同的两点，则．

其中真命题的个数为（ ）

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】

由新定义，利用导数求出函数y＝sinx、y＝x2在点A与点B之间的“弯曲度”判断①、③正确；举例说明②是正确的；求出曲线y＝ex上不同两点A（x1，y1），B（x2，y2）之间的“弯曲度”，判断④错误．

对于①，由y＝sinx，得y′＝cosx，

则kA＝cos1，kB＝cos（﹣1）＝cos1，则|kA﹣kB|＝0，即φ（A，B）＝0，①正确；

对于②，如y＝1时，y′＝0，则φ（A，B）＝0，②正确；

对于③，抛物线y＝x2的导数为y′＝2x，yA＝xA2，yB＝xB2，

∴yA﹣yB＝xA2﹣xB2＝（xA﹣xB）（xA+xB），

则φ（A，B）2，③正确；

对于④，由y＝ex，得y′＝ex，φ（A，B），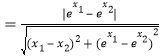

由不同两点A（x1，y1），B（x2，y2），可得φ（A，B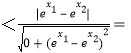）1，∴④错误；

综上所述，正确的命题序号是①②③．

故选：C．