题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,若曲线
,若曲线![]() ,
,![]() 有公共点
有公共点![]() ,且在点
,且在点![]() 处的切线相同,求
处的切线相同,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求出原函数的导函数,得到导函数的零点,由导函数的零点对函数定义域分段,再由导函数在不同区间段内的符号可得原函数的单调性;
(Ⅱ)设点P的横坐标为x0(x0>0),由题意得 ,得到
,得到![]() (a>0).设
(a>0).设![]() ,利用导数求其最大值得答案.
,利用导数求其最大值得答案.
(Ⅰ)![]() 的定义域为
的定义域为![]() .
.
![]()
![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅱ)设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
由题意得
由![]() 得
得![]() 或
或![]() (舍).
(舍).
所以![]()
![]() .
.
设![]() ,则
,则
![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当 ![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 在
在![]() 的最大值为
的最大值为![]() ,
,
即![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
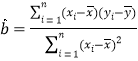
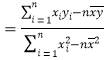 ,
,![]() .
.