题目内容
19.直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
分析 由题意首先求出第一象限的交点,然后利用定积分表示围成的图形的面积,然后计算即可.
解答 解:先根据题意画出图形,两个图形在第一象限的交点为(2,8),
所以曲线y=x3与直线y=4x在第一象限所围成的图形的面积是∫02(4x-x3)dx,
而∫02(4x-x3)dx=(2x2-$\frac{1}{4}$x4)|02=8-4=4
∴曲封闭图形的面积是4,
故选B.
点评 本题考查学生利用定积分求曲边梯形的面积,会求出原函数的能力,同时考查了数形结合的思想,属于基础题.

练习册系列答案
相关题目
10.设Sn是公差不为0的等差数列{an}的前n项和,S3=a22,且S1,S2,S4成等比数列,则a10=( )
| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
14.甲、乙两人分别从四种不同品牌的商品中选择两种,则甲、乙所选的商品中恰有一种品牌相同的选法种数是( )
| A. | 30 | B. | 24 | C. | 12 | D. | 6 |
4.函数y=2sinx,x∈[0,2π]与y=$\frac{3}{2}$的交点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.如果a<b<0,那么下列不成立的是( )
| A. | a2>b2 | B. | a3>b3 | C. | $\sqrt{{a}^{2}}$>$\sqrt{{b}^{2}}$ | D. | a-b<b-a |
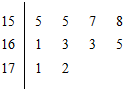 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.