题目内容
20.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=2$\overrightarrow{DB}$,则$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$其中m,n分别为( )| A. | m=$\frac{1}{3}$,n=-$\frac{2}{3}$ | B. | m=$\frac{1}{3}$,n=$\frac{2}{3}$ | C. | m=-$\frac{2}{3}$,n=$\frac{1}{3}$ | D. | m=$\frac{2}{3}$,n=$\frac{1}{3}$ |
分析 由$\overrightarrow{AD}$=2$\overrightarrow{DB}$,可得$\overrightarrow{CD}-\overrightarrow{CA}=2(\overrightarrow{CB}-\overrightarrow{CD})$,即$\overrightarrow{CD}$=$\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB}$,与$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$比较即可得出m,n.
解答 解:如图所示,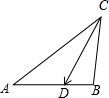
∵$\overrightarrow{AD}=2\overrightarrow{DB}$,
∴$\overrightarrow{CD}-\overrightarrow{AD}=2(\overrightarrow{CB}-\overrightarrow{CD})$,
即$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB}$.
∵$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$,
∴m=$\frac{1}{3}$,n=$\frac{2}{3}$,
故选:B.
点评 本题考查了向量的三角形运算法则、平面向量的基本定理,属于基础题.

练习册系列答案
相关题目
14.甲、乙两人分别从四种不同品牌的商品中选择两种,则甲、乙所选的商品中恰有一种品牌相同的选法种数是( )
| A. | 30 | B. | 24 | C. | 12 | D. | 6 |
11.设命题p:?x∈R,x2+x+1<0;命题q:?x∈[1,2],x2-1≥0;则以下命题是真命题的是( )
| A. | ¬p∧¬q | B. | p∨¬q | C. | ¬p∧q | D. | p∧q |
8.已知向量$\vec a$=(2cosα,2sinα),$\vec b$=(3cosβ,3sinβ),$\vec a$与$\vec b$的夹角为60°,则直线$xcosα-ysinα+\frac{1}{2}=0$与圆${(x-cosβ)^2}+{(y+sinβ)^2}=\frac{1}{2}$的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 随α,β的值而定 |
5.如果a<b<0,那么下列不成立的是( )
| A. | a2>b2 | B. | a3>b3 | C. | $\sqrt{{a}^{2}}$>$\sqrt{{b}^{2}}$ | D. | a-b<b-a |
10.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|的值为( )
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8$\sqrt{2}$ | D. | 8 |
