题目内容
2.已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=1024,则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值为( )| A. | 21 | B. | 35 | C. | 56 | D. | 210 |
分析 由条件利用二项式定理求得n=5,再利用组合数的计算公式求得C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值.
解答 解:∵已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=(1+3)n=1024,∴n=5,
则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$=${C}_{6}^{2}$+${C}_{6}^{3}$=15+20=35,
故选:B.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,组合数的计算公式,属于基础题.

练习册系列答案
相关题目
13.设函数f(x)=sinx+cosx,把f(x)的图象向右平移m(m>0)个单位长度后图象恰好为函数g(x)=sinx-cosx的图象,则m的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
10.设Sn是公差不为0的等差数列{an}的前n项和,S3=a22,且S1,S2,S4成等比数列,则a10=( )
| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
17.已知i为虚数单位,且z=i(1-i),则复数z的共轭复数为( )
| A. | -1+i | B. | 1-i | C. | 1+i | D. | -1-i |
14.甲、乙两人分别从四种不同品牌的商品中选择两种,则甲、乙所选的商品中恰有一种品牌相同的选法种数是( )
| A. | 30 | B. | 24 | C. | 12 | D. | 6 |
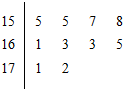 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.