题目内容
直线 与圆
与圆 交于
交于 、
、 两点,且
两点,且 、
、 关于直线
关于直线 对称,则弦
对称,则弦 的长为
的长为
| A. 2 | B.3 | C. 4 | D.5 |
C
解析试题分析:因为M,N关于直线 对称,所以,直线MN的斜率为1,且圆心(
对称,所以,直线MN的斜率为1,且圆心( )过直线
)过直线 ,那么
,那么 ,即m=2,n=-2,
,即m=2,n=-2,
直线MN的方程为 ,代入圆方程并求的两点为(2,2),(-2,-2)
,代入圆方程并求的两点为(2,2),(-2,-2)
所以|MN|=4,故选C。
考点:对称问题,直线与圆的位置关系。
点评:中档题,本题充分利用对称性,建立了m,n的方程组,从而通过联立直线方程、圆的方程之方程组,求得弦长。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
在平面直角坐标系 中,圆
中,圆 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,则直线
,则直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相离 | B.相交 | C.相切 | D.相切或相交 |
M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
直线 与圆
与圆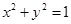 交于不同两点
交于不同两点 、
、 ,
, 为坐标原点,则“
为坐标原点,则“ ”是“向量
”是“向量 、
、 满足
满足 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合 ,集合
,集合 ,若
,若 ,则实数
,则实数 可以取的一个值是( )
可以取的一个值是( )
A. | B. | C. | D. |
若函数 的图象在x=0处的切线
的图象在x=0处的切线 与圆
与圆 相离,则
相离,则 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.在圆外 | B.在圆内 | C.在圆上 | D.不能确定 |




 ,在上任取一点
,在上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 .设是长为2的线段,点集
.设是长为2的线段,点集 所表示图形的面积为( )
所表示图形的面积为( )


