题目内容
M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
C
解析试题分析:由圆的方程得到圆心坐标为(0,0),半径r=a,
由M为圆内一点得,
则圆心到已知直线的距离d= =a=r,
=a=r,
所以,直线与圆相离,故选C。
考点:直线与圆的位置关系
点评:中档题,直线与圆的位置关系的判断方法,常常运用点到直线的距离公式及“特征直角三角形”。

练习册系列答案
相关题目
若直线 与曲线
与曲线 有交点,则( )
有交点,则( )
A. 有最大值 有最大值 ,最小值 ,最小值 | B. 有最大值 有最大值 ,最小值 ,最小值 |
C. 有最大值0,最小值 有最大值0,最小值  | D. 有最大值0,最小值 有最大值0,最小值 |
曲线 与直线
与直线 有公共点的充要条件是( )
有公共点的充要条件是( )
A. | B. | C. | D. |
已知圆 在曲线
在曲线 的内部,则半径
的内部,则半径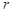 的范围是( )
的范围是( )
A.0<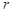 < < | B.0<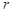 <2 <2 | C.0<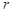 <2 <2 | D.0<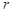 <4 <4 |
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
已知圆C经过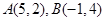
 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是
A.  | B.  |
C.  | D. |
直线 与圆
与圆 交于
交于 、
、 两点,且
两点,且 、
、 关于直线
关于直线 对称,则弦
对称,则弦 的长为
的长为
| A. 2 | B.3 | C. 4 | D.5 |
直线 被圆
被圆 截得的线段的长为( )
截得的线段的长为( )
| A.2 | B. | C. | D.1 |



