题目内容
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D. |
B
解析试题分析:∵圆心(4,0)到直线 的距离d=
的距离d= ,由圆中的重要三角形知,弦长为2
,由圆中的重要三角形知,弦长为2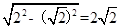 ,故选B
,故选B
考点:本题考查了弦长的求解
点评:对弦长的计算有两种方法:一用弦长公式 。二用勾股定理
。二用勾股定理

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
已知圆 :
: +
+ =1,圆
=1,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的方程为( )
的方程为( )
A. + + =1 =1 | B.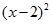 + + =1 =1 |
C. + + =1 =1 | D.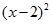 + + =1 =1 |
已知圆 在曲线
在曲线 的内部,则半径
的内部,则半径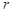 的范围是( )
的范围是( )
A.0<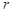 < < | B.0<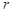 <2 <2 | C.0<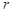 <2 <2 | D.0<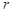 <4 <4 |
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
已知圆C经过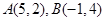
 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是
A.  | B.  |
C.  | D. |
直线 与圆
与圆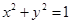 的位置关系为( )
的位置关系为( )
| A.相切 | B.相交但直线不过圆心 |
| C.直线过圆心 | D.相离 |
直线 与圆
与圆 交于
交于 、
、 两点,且
两点,且 、
、 关于直线
关于直线 对称,则弦
对称,则弦 的长为
的长为
| A. 2 | B.3 | C. 4 | D.5 |
已知圆 ,若过圆内一点
,若过圆内一点 的最长弦为
的最长弦为 ,最短弦为
,最短弦为 ;则四边形
;则四边形 的面积为( )
的面积为( )
A. | B. | C. | D. |
已知圆的方程为(x-3)2+y2=9,则圆心坐标为( )
| A.(3,0) | B.(-3,0) | C.(0,3) | D.(0,-3) |