题目内容
11.如图所示,表示阴影部分的二元一次不等式组是( )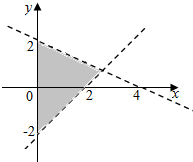
| A. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4>0\\ x≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4>0\\ x≥0\end{array}\right.$ |
分析 求出对应的直线方程,结合二元一次不等式与平面区域的关系进行求解即可.
解答 解:过(2,0),(0,-2)的直线方程为$\frac{x}{2}+\frac{y}{-2}=1$,即x-y-2=0,
过(4,0),(0,2)的直线方程为$\frac{x}{4}$+$\frac{y}{2}$=1,即x+2y-4=0,
则对应的区域在y轴的右侧,x-y-2=0的上方,x+2y-4=0的下方,
则对应的不等式组为$\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$,
故选:B
点评 本题主要考查二元一次不等式组的确定,求出直线方程结合二元一次不等式组表示平面区域的性质是解决本题的关键.

练习册系列答案
相关题目
1.从一批含有13只正品,2只次品的产品中,不放回地任取3件,则取得次品数为1件的概率是( )
| A. | $\frac{32}{35}$ | B. | $\frac{12}{35}$ | C. | $\frac{3}{35}$ | D. | $\frac{2}{35}$ |
1.已知数列{an}中,a3=2,a7=1,且数列{$\frac{1}{{{a_n}+1}}$}为等差数列,则a8=( )
| A. | -$\frac{7}{11}$ | B. | $\frac{13}{11}$ | C. | $\frac{11}{13}$ | D. | -$\frac{5}{7}$ |