题目内容
13.设变量x,y满足$\left\{\begin{array}{l}{x-y≥-1}\\{x+y≥1}\\{3x-y≤3}\end{array}\right.$,则w=4x+y的最大值为( )| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
分析 作出不等式组对应的平面区域,设y=-4x+w,利用W的几何意义,即可得到结论.
解答 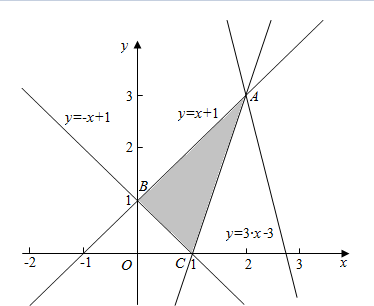 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
设w=4x+y,即y=-4x+w,
平移直线y=-4x+w,由图象可知当直线y=-4x+w经过点A(2,3)时,直线y=-4x+w的截距最大,此时w最大,
即w=11,
故选:B.
点评 本题主要考查线性规划的应用,利用z的几何意义,结合数形结合是解决本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
1.从一批含有13只正品,2只次品的产品中,不放回地任取3件,则取得次品数为1件的概率是( )
| A. | $\frac{32}{35}$ | B. | $\frac{12}{35}$ | C. | $\frac{3}{35}$ | D. | $\frac{2}{35}$ |
8.AB是圆O内的一条弦,圆O半径是5,且圆心到AB的距离为3,则弦AB的长度为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
5.已知全集U={a,b,c,d,e},集合A={b,c},∁UB={c,d},则(∁UA)∩B等于( )
| A. | {a,e} | B. | {b,c,d} | C. | {a,c,e} | D. | {c} |
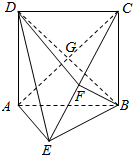 如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G
如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G