题目内容
18.如果我们现在手里有6本书,按下列要求各有多少种不同的排法:(1)6本书有1---6的编号,排成一排,1号和2号必须相邻;
(2)6本书有1---6的编号,排成一排,1号和2号不能相邻;
(3)6本书厚度各不相同,取出3本排成一排,从左到右厚度依次降低.
分析 (1)根据题意,用捆绑法分析:①、将1、2号看成一个元素,并考虑其顺序,②、将这个元素与剩下的4本数进行全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(2)根据题意,由插空法分析:①、将出1、2号之外的4本书全排列,②、这4本书排好后,有5个空位,在5个空位中任选2个,安排1、2号,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(3)根据题意,分2步进行分析:①、先在6本书中选取3本,②、分析取出的3本按从要求顺序的情况数目,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:(1)根据题意,用捆绑法分析:
①、将1、2号看成一个元素,考虑其顺序,有A22种情况,
②、将这个元素与剩下的4本数进行全排列,有A53种情况,
则1号和2号必须相邻的排法有$A_2^2A_5^5=240$种;
(2)根据题意,由插空法分析:
①、将出1、2号之外的4本书全排列,有A44种情况,
②、这4本书排好后,有5个空位,在5个空位中任选2个,安排1、2号,有A52种安排方法,
则1号和2号不能相邻的排法有$A_4^4A_5^2=480$种;
(3)根据题意,分2步进行分析:
①、先在6本书中选取3本,有C63种选取方法,
②、由于6本书厚度各不相同,则取出的3本按从左到右厚度依次降低的顺序只有1种情况,
则满足条件的排法有1×$C_6^3=20$种.
点评 本题考查排列、组合的运用,需要掌握常见问题的处理方法,如相邻问题用捆绑法,不能相邻问题用插空法.

练习册系列答案
相关题目
8.AB是圆O内的一条弦,圆O半径是5,且圆心到AB的距离为3,则弦AB的长度为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
9.函数f(x)=ex-ex在[0,2]上的最大值为( )
| A. | 0 | B. | 1 | C. | e-2 | D. | e(e-2) |
13.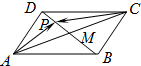 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )| A. | -$\frac{5}{16}$ | B. | -$\frac{15}{16}$ | C. | -$\frac{25}{16}$ | D. | -$\frac{27}{16}$ |
7.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |