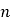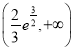题目内容
【题目】(12分)
已知抛物线![]() 的焦点F与椭圆
的焦点F与椭圆![]() 的一个焦点重合,点
的一个焦点重合,点![]() 在抛物线上,过焦点F的直线l交抛物线于A,B两点.
在抛物线上,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的标准方程以及![]() 的值.
的值.
(2)记抛物线的准线![]() 轴交于点H,试问是否存在常数
轴交于点H,试问是否存在常数![]() ,使得
,使得![]() ,且
,且![]() 都成立.若存在,求出
都成立.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() .
.
(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,可求得
的一个焦点重合,可求得![]() 的值,即可得抛物线
的值,即可得抛物线![]() 的标准方程,从而可求得
的标准方程,从而可求得![]() ,再根据抛物线的定义即可求得
,再根据抛物线的定义即可求得![]() 的值;(2)设
的值;(2)设![]() :
:![]() ,
,![]() ,
,![]() ,联立
,联立![]() ,根据韦达定理可得
,根据韦达定理可得![]() 与
与![]() 的值,再根据
的值,再根据![]() ,可得
,可得![]() 与
与![]() 的关系,再将
的关系,再将![]() 化简,即可求得
化简,即可求得![]() 的值.
的值.
试题解析:(1)依题意得椭圆![]() 的焦点为
的焦点为![]() ,即
,即![]() ,故
,故![]() ,则
,则![]() ,故抛物线
,故抛物线![]() 的标准方程为
的标准方程为![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,故
,故![]() .
.
(2)设![]() ,联立
,联立![]() ,得
,得![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,则
,则![]() ,即
,即![]() ,代入
,代入![]() 式,得
式,得
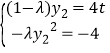 ,消去
,消去![]() ,得
,得![]() .
.
又![]() ,故
,故![]()
![]()
![]()
![]()
![]() .
.
由![]() ,解得
,解得![]() 或
或![]() (舍去),故
(舍去),故![]() 或
或![]() .
.
即存在![]() 满足条件,且
满足条件,且![]() 的值为
的值为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目