Question

【题目】已知函数，，若有最小值，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

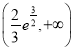
【答案】C

【解析】

对函数求导得出，由题意得出函数在上存在极小值点，然后对参数分类讨论，在时，函数单调递增，无最小值；在时，根据函数的单调性得出，从而求出实数的取值范围.

，，

构造函数，其中，则.

①当时，对任意的，，则函数在上单调递减，

此时，，则对任意的，.

此时，函数在区间上单调递增，无最小值；

②当时，解方程，得.

当时，，当时，，

此时，.

（i）当时，即当时，则对任意的，，

此时，函数在区间上单调递增，无最小值；

（ii）当时，即当时，，当时，，

由零点存在定理可知，存在和，使得，

即，且当和时，，此时，；

当时，，此时，.

所以，函数在处取得极大值，在取得极小值，

由题意可知，，

，

可得，又，可得，构造函数，其中，

则，此时，函数在区间上单调递增，

当时，则，.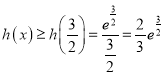

因此，实数的取值范围是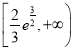，故选：C.