题目内容
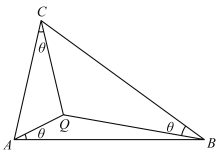
【题目】三角形的勃劳卡德点是以法国军官亨利·勃劳卡德(Henri.Brocard)命名的,他在1875年曾描述过这一事实,即:对任何一个三角形都存在唯一的角![]() ,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
,即勃劳卡德角,使得图中连接三个顶点的线相交于勃劳卡德点Q,如图所示.
(1)研究发现:等腰直角三角形中![]() ,若
,若![]() 是斜边
是斜边![]() 的等腰直角三角形,求线段
的等腰直角三角形,求线段![]() 的长度;
的长度;
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() 中,若线段
中,若线段![]() ,
,![]() ,
,![]() 的长度是1为首项,公比为q(
的长度是1为首项,公比为q(![]() )的等比数列,当
)的等比数列,当![]() 时,求公比q的值.
时,求公比q的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可得![]() ,
,![]() ,然后在
,然后在![]() 中利用正弦定理可求出
中利用正弦定理可求出![]() 的长;
的长;
(2)在![]() 中由正弦定理求得
中由正弦定理求得![]() ,再利用
,再利用![]() 求出
求出![]() ,列出等式求出
,列出等式求出![]() 的值;
的值;
(3)由等比数列求出![]() ,
,![]() ,在
,在![]() 和
和![]() 中由正弦定理得
中由正弦定理得![]() ,
,![]() ,由此可得出
,由此可得出![]() ,得到
,得到![]() ,再由正弦定理得
,再由正弦定理得![]() ,再对此式化简得
,再对此式化简得![]() ,然后在表示出
,然后在表示出![]() 的值代入化简可得结果
的值代入化简可得结果
(1)由题意可知,![]() ,
,![]() ,于是
,于是![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
得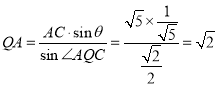 .
.
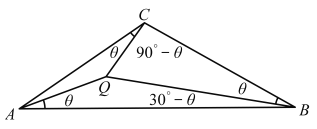
(2)由题意可得![]() ,
,![]() ,
,![]()
由已知,![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,
在![]() 中,有正弦定理得
中,有正弦定理得![]() ,
,
在![]() 中,
中,![]()
所以![]() ,解得
,解得![]() .
.
(2)设![]() 的三边a,b,c的对角分别为A,B,C.
的三边a,b,c的对角分别为A,B,C.
由于线段![]() ,
,![]() ,
,![]() 的长度是1为首项,则
的长度是1为首项,则![]() ,
,![]()
在![]() 和
和![]() 中由正弦定理得
中由正弦定理得![]() ,
,![]()
所以![]() ,于是
,于是![]() ,且
,且![]()
所以![]() ,所以
,所以![]() ,所以
,所以![]()
注意到![]() ,
,![]()
在![]() 和
和![]() 中由正弦定理得
中由正弦定理得![]() ①
①
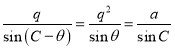 ②
②
①![]() ②得
②得![]() ,即
,即![]() ,且有
,且有![]() (
(![]() 是已知的)
是已知的)
展开得![]()
又等腰三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 代入得
代入得
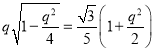 ,令
,令![]() ,代入平方整理得
,代入平方整理得![]()
解得![]() 或
或![]() (舍去),所以
(舍去),所以![]() .
.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目