题目内容
【题目】函数
（其中
）的部分图象如图所示，把函数
的图像向右平移
个单位长度，再向下平移1个单位，得到函数
的图像.
（1）当
时，求的值域
（2）令
，若对任意
都有
恒成立，求
的最大值
【答案】（1）
（2）
【解析】
（1）根据图象的最低点求得
的值，根据四分之一周期求得
的值，根据点
求得
的值，由此求得函数
的解析式，进而根据图象平移变换求得
的解析式，并由此求得
时的值域.（2）先求得的值域，由此求得
的值域.令
对题目所给不等式换元，根据二次函数的性质列不等式组，解不等式组求得
的取值范围，由此求得的最大值.
（1）根据图象可知
代入得，
，
把函数
的图像向右平移
个单位长度，再向下平移1个单位，得到函数
，
设
，则
，
此时
，
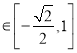所以值域为.
（2）由（1）可知
对任意
都有
恒成立
令，
，是关于
的二次函数，开口向上
则
恒成立
而
的最大值，在
或
时取到最大值
则
，
，
解得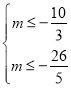
所以
，则的最大值为.
练习册系列答案
相关题目
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时，便会想起电影《泰坦尼克号》中一暮暮感人画面，让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济，更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型
比例重新修建.为了了解该旅游开发在大众中的熟知度，随机从本市
岁的人群中抽取了
人，得到各年龄段人数的频率分布直方图如图所示，现让他们回答问题“该旅游开发将在我市哪个地方建成？”，统计结果如下表所示：
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
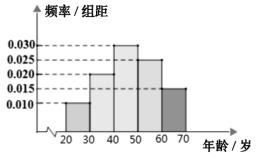
（1）求出
的值；
（2）从第
组回答正确的人中用分层抽样的方法抽取
人，求第组每组抽取的人数；
（3）在（2）中抽取的
人中随机抽取
人，求所抽取的人中恰好没有年龄在
段的概率.
