题目内容
【题目】如果对定义在R上的函数f（x）对任意两个不相等的实数x1 ， x2 ， 都有（x1﹣x2）[f（x1）﹣f（x2）]＞0，则称函数f（x）为“H函数”．给出下列函数①y=﹣x3+x+1；②y=3x﹣2（sinx﹣cosx）；③y=ex+1；④ 
．其中“H函数”的个数为（ ）
A.1
B.2
C.3
D.4
【答案】B
【解析】解：若函数f（x）对任意两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＞0，
则等价为函数f（x）为增函数，
则①y=﹣x3+x+1；
则y′=﹣3x2+1，由f′（x）＞0得﹣ 
＜x＜ ，则函数的单调递增区间为不是（﹣∞，+∞），不满足条件．②y=3x﹣2（sinx﹣cosx）；
则y′=3﹣2 
sin（x+ 
）＞0恒成立，即函数在（﹣∞，+∞）上为增函数满足条件．③y=ex+1在（﹣∞，+∞）为增函数，满足条件；④ 
为偶函数，在（﹣∞，+∞）不是单调递增函数，不满足条件．
故“H函数”的个数为2个，
故选：B．
练习册系列答案
相关题目
【题目】某火锅店为了解气温对营业额的影响，随机记录了该店1月份中5天的日营业额y（单位：千元）与该地当日最低气温x（单位：℃）的数据，如表：
x | 2 | 8 | 9 | 11 | 5 |
y | 12 | 8 | 8 | 7 | 10 |
（1）求y关于x的回归方程 
；
（2）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额． （附：回归方程 中， 
= 
= 
， 
= 
﹣ 
．）
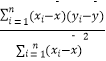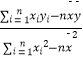