Question

【题目】在二项式（ + ）n展开式中，前三项的系数成等差数列． 求：（1）展开式中各项系数和；
【答案】解：由题意得2 × =1+ × ，
化为：n2﹣9n+8=0，解得n=1（舍去）或8．
∴n=8．
在 中，令x=1，可得展开式中各项系数和= = ．
（1）展开式中系数最大的项．

Answer 1

【答案】
（1）解： 设 展 开 式 中 第 r+1 项 系 数 最 大，

则 Tr+1= = ，

则 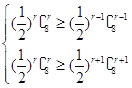，解得 2≤r≤3．

因 此 r=2 或 3，即 展 开 式 中 第 3 项 和 第 4 项 系 数 最 大，且 T3= =7 ．

T4= =7 ．

∴展开式中系数最大的项分别为：7 ，7 ．

【解析】（Ⅰ） 由 题 意 得 2 × =1+ × ，化为：n2﹣9n+8=0，解得n=8．在 中，令x=1，可得展开式中各项系数和．（Ⅱ） 设 展 开 式 中 第 r+1 项 系 数 最 大，Tr+1= = ，则 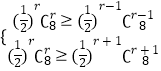，解得r即可得出．