题目内容
19．袋中有5个球，其中有彩色球2个．甲、乙二人先后依次从袋中取球，每次取后不放回，规定先取出彩色球者获胜．则甲获胜的概率为$\frac{3}{5}$．（以整数比作答）分析 甲能取胜包括两种情况：①甲第一次取到彩球，②甲第一次没取到彩球，乙第二次没取到彩球甲第三次取到彩球，可求．
解答 解：甲能取胜包括两种情况：①甲第一次取到彩球，
②甲第一次没取到彩球，乙第二次没取到彩球甲第三次取到彩球，
甲获胜的概率为P=$\frac{2}{5}+\frac{3}{5}×\frac{2}{4}×\frac{2}{3}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$
点评 本题主要了实际问题中的概率求解，解题的关键是把所要求解的时事件所包含的问题弄清楚．
练习册系列答案
阅读快车系列答案
相关题目
9．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与抛物线y2=4x的焦点重合，则a+b的最大值为（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{\sqrt{2}}{2}$ | D． | 2$\sqrt{2}$ |
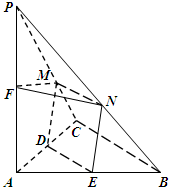如图，在三棱锥P-ABC中，PA⊥平面ABC，2AC=2BC=PC=2，AC⊥BC，D、E、F分别为AC、AB、AP的中点，M、N分别为线段PC、PB上的动点，且有MN∥BC．