题目内容
2．已知矩阵M=$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$，β=$[\begin{array}{l}{3}\\{5}\end{array}]$，计算M2β．分析 通过M=$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$可得M2=$[\begin{array}{l}{5}&{4}\\{4}&{5}\end{array}]$，进而可得M2β=$[\begin{array}{l}{35}\\{37}\end{array}]$．
解答 解：∵M=$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$，∴M2=$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$$[\begin{array}{l}{2}&{1}\\{1}&{2}\end{array}]$=$[\begin{array}{l}{5}&{4}\\{4}&{5}\end{array}]$，
又∵β=$[\begin{array}{l}{3}\\{5}\end{array}]$，∴M2β=$[\begin{array}{l}{5}&{4}\\{4}&{5}\end{array}]$$[\begin{array}{l}{3}\\{5}\end{array}]$=$[\begin{array}{l}{35}\\{37}\end{array}]$．
点评 本题考查矩阵的计算，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
如图，直线PQ与⊙O相切于点A，AB是⊙O的弦，∠PAB的平分线AC交⊙O于点C，连结CB，并延长与直线PQ相交于点Q，若AQ=6，AC=5．
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内，其中顶点P、C、Q、D分别在矩形的四条边上．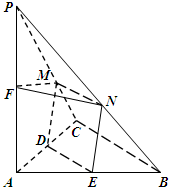
如图，在三棱锥P-ABC中，PA⊥平面ABC，2AC=2BC=PC=2，AC⊥BC，D、E、F分别为AC、AB、AP的中点，M、N分别为线段PC、PB上的动点，且有MN∥BC．