题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,顶点
,顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,椭圆
,椭圆![]() 内接四边形
内接四边形![]() (点
(点![]() 在椭圆上)的对角线
在椭圆上)的对角线![]() 相交于点
相交于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据椭圆的离心率及顶点到直线的距离建立a,b,c的方程,即可求出椭圆标准方程;(2)可先求出直线![]() 的方程为
的方程为![]() ,再求出弦长
,再求出弦长![]() ,再求出点C到直线AB的距离即可写出三角形面积.
,再求出点C到直线AB的距离即可写出三角形面积.
试题解析:
(1)解:由题意知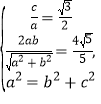 ,解得
,解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)设点![]() ,有
,有![]() ①
①
因为![]() ,且
,且![]()
所以点![]() 的坐标为
的坐标为![]()
因为点![]() 在椭圆
在椭圆![]() 上,所以将点
上,所以将点![]() 坐标代入
坐标代入![]() 种
种
得![]() ②
②
由①、②得![]()
设点![]() ,同理可得
,同理可得![]()
因为![]() 都满足方程
都满足方程![]()
所以直线![]() 的方程为
的方程为![]()
设点![]() ,解得
,解得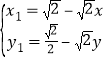
代入![]() 得
得![]()
同理点![]() 也满足方程
也满足方程![]()
所以直线![]() 的方程为
的方程为![]()
因为![]()
可得![]()
![]() 到直线
到直线![]() 的距离为
的距离为![]()
所以![]() 的面积等于
的面积等于![]() .
.

【题目】2017年被称为”新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进.辽宁地区也将于2020年开启新高考模式,今年秋季入学的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为自已将来高考“语数外+3”新高考方案中的“3”.某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模找拟选科数据”调查,每个学生只能从表格中的20种课程组合选择一种学习.模拟选课数据统计如下表 :
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物证历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | … | 40人 | … | … |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | … | … | … | … | … | … | 200人 |
为了解学生成绩与学生模拟选课情况之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)从选择学习物理且学习化学的学生中随机抽取3人,求这3人中至少有2天要学习生物的概率;
(2)从选择学习物理且学习化学的学生中随机抽取3人,记这3人中要学习生物的人数为![]() ,要学习政治的人数为
,要学习政治的人数为![]() ,设随机变量
,设随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
