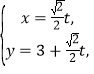ЬтФПФкШн
ЁОЬтФПЁП2017ФъБЛГЦЮЊЁБаТИпПМдЊФъЁБ,ЫцзХЩЯКЃЁЂеуНСНЕиЫГРћЪЕЪЉЁАгяЪ§Эт+3ЁБаТИпПМЗНАИ,аТвЛТжЕФИпПМИФИяЛЙНЋМЬајдкШЋЙњЭЦНј.СЩФўЕиЧјвВНЋгк2020ФъПЊЦєаТИпПМФЃЪН,НёФъЧяМОШыбЇЕФИпвЛаТЩњНЋУцСйДгЮяРэЁЂЛЏбЇЁЂЩњЮяЁЂеўжЮЁЂРњЪЗЁЂЕиРэЕШ6ПЦжаШЮбЁШ§ПЦ(ЙВ20жжбЁЗЈ)зїЮЊздвбНЋРДИпПМЁАгяЪ§Эт+3ЁБаТИпПМЗНАИжаЕФЁА3ЁБ.ФГЕиЧјЮЊСЫЫГРћгНгаТИпПМИФИя,дкФГбЇаЃРэПЦАрЕФ200УћбЇЩњжаНјааСЫЁАбЇЩњФЃевФтбЁПЦЪ§ОнЁБЕїВщ,УПИібЇЩњжЛФмДгБэИёжаЕФ20жжПЮГЬзщКЯбЁдёвЛжжбЇЯА.ФЃФтбЁПЮЪ§ОнЭГМЦШчЯТБэ ЃК
ађКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
зщКЯбЇПЦ | ЮяЛЏЩњ | ЮяЛЏеў | ЮяЛЏРњ | ЮяЛЏЕи | ЮяЩњеў | ЮяЩњРњ | ЮяЩњЕи |
ШЫЪ§ | 20ШЫ | 5ШЫ | 10ШЫ | 10ШЫ | 10ШЫ | 15ШЫ | 10ШЫ |
ађКХ | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
зщКЯбЇПЦ | ЮяжЄРњ | ЮяеўЕи | ЮяРњЕи | ЛЏЩњеў | ЛЏЩњРњ | ЛЏЩњЕи | ЛЏеўРњ |
ШЫЪ§ | 5ШЫ | 0ШЫ | 5ШЫ | Ё | 40ШЫ | Ё | Ё |
ађКХ | 15 | 16 | 17 | 18 | 19 | 20 | |
зщКЯбЇПЦ | ЛЏеўЕи | ЛЏРњЕи | ЩњеўРњ | ЩњеўЕи | ЩњРњЕи | еўРњЕи | змМЦ |
ШЫЪ§ | Ё | Ё | Ё | Ё | Ё | Ё | 200ШЫ |
ЮЊСЫНтбЇЩњГЩМЈгыбЇЩњФЃФтбЁПЮЧщПіжЎМфЕФЙиЯЕ,гУЗжВуГщбљЕФЗНЗЈДгет200УћбЇЩњжаГщШЁ40ШЫЕФбљБОНјааЗжЮі.
(1)ДгбЁдёбЇЯАЮяРэЧвбЇЯАЛЏбЇЕФбЇЩњжаЫцЛњГщШЁ3ШЫ,Чѓет3ШЫжажСЩйга2ЬьвЊбЇЯАЩњЮяЕФИХТЪЃЛ
(2)ДгбЁдёбЇЯАЮяРэЧвбЇЯАЛЏбЇЕФбЇЩњжаЫцЛњГщШЁ3ШЫ,МЧет3ШЫжавЊбЇЯАЩњЮяЕФШЫЪ§ЮЊ![]() ,вЊбЇЯАеўжЮЕФШЫЪ§ЮЊ
,вЊбЇЯАеўжЮЕФШЫЪ§ЮЊ![]() ,ЩшЫцЛњБфСП
,ЩшЫцЛњБфСП![]() ,ЧѓЫцЛњБфСП
,ЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЁОД№АИЁП(1)![]() ЃЛ(2)Д№АИМћНтЮі.
ЃЛ(2)Д№АИМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЗжБ№МЦЫу2ШЫбЁЩњЮяКЭШ§ШЫбЁЩњЮяЕФбЁЗЈЃЌгЩМгЗЈдРэПЩЕУЙВ34жжЃЌДгЖјМЦЫуГіЦфИХТЪЃЛЃЈ2ЃЉЮяЛЏЩњзщКЯга4ШЫ,![]() ЕФПЩФмШЁжЕЮЊ0,1,2,3,ЮяЛЏеўзщКЯ1ШЫ,
ЕФПЩФмШЁжЕЮЊ0,1,2,3,ЮяЛЏеўзщКЯ1ШЫ,![]() ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ
ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ![]() ЕФПЩФмШЁжЕЮЊ-1ЃЌ0ЃЌ1,2ЃЌ3.ИљОнЙХЕфИХаЭЃЌЗжБ№ЧѓЦфИХТЪМДПЩЕУГіЗжВМСаМАЦкЭћ.
ЕФПЩФмШЁжЕЮЊ-1ЃЌ0ЃЌ1,2ЃЌ3.ИљОнЙХЕфИХаЭЃЌЗжБ№ЧѓЦфИХТЪМДПЩЕУГіЗжВМСаМАЦкЭћ.
ЪдЬтНтЮіЃК
(1)бЁдёбЇЯАЮяРэЧвбЇЯАЛЏбЇЕФбЇЩњга9ШЫ,ЦфжабЇЯАЩњЮяЕФга4ШЫДг9ШЫжабЁ3ШЫЙВга![]() жжбЁЗЈ,га2ШЫбЁдёЩњЮяЕФбЁЗЈЙВга
жжбЁЗЈ,га2ШЫбЁдёЩњЮяЕФбЁЗЈЙВга![]() жж,га3ШЫбЁдёЩњЮяЕФбЁЗЈга
жж,га3ШЫбЁдёЩњЮяЕФбЁЗЈга![]() жжЃЌЫљвджСЩйга2ШЫбЁдёЩњЮяЕФИХТЪЮЊ
жжЃЌЫљвджСЩйга2ШЫбЁдёЩњЮяЕФИХТЪЮЊ![]() .
.
(2)ЮяЛЏЩњзщКЯга4ШЫ,![]() ЕФПЩФмШЁжЕЮЊ0,1,2,3,ЮяЛЏеўзщКЯ1ШЫ,
ЕФПЩФмШЁжЕЮЊ0,1,2,3,ЮяЛЏеўзщКЯ1ШЫ,![]() ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ
ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ![]() ЕФПЩФмШЁжЕЮЊ-1ЃЌ0ЃЌ1,2ЃЌ3.
ЕФПЩФмШЁжЕЮЊ-1ЃЌ0ЃЌ1,2ЃЌ3.
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ
![]() ЕФЗжВМСа
ЕФЗжВМСа
| -1 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() .
.