题目内容
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线
是抛物线![]() 上一点,且
上一点,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)过点![]() 作两条互相垂直的直线,与抛物线
作两条互相垂直的直线,与抛物线![]() 的另一交点分别是
的另一交点分别是![]() ,
,![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的方程;
的方程;
②若![]() 的面积为12,求
的面积为12,求![]() 的斜率.
的斜率.
【答案】(1)![]() ,
,![]() (2)①
(2)①![]() ②
②![]() 或
或![]()
【解析】
(1)直接利用抛物线方程,结合定义求p的值;然后求解t;
(2)①直线AB的斜率为![]() ,设出方程,A、B坐标,与抛物线联立,然后求AB的方程;
,设出方程,A、B坐标,与抛物线联立,然后求AB的方程;
②求出三角形的面积的表达式,结合△ABC的面积为12,求出m,然后求AB的斜率.
解:(1)由抛物线定义得![]() ,
,![]()
![]() ,
,![]()
(2)设![]() 方程为
方程为![]() ,
,![]() ,
,![]()
与抛物线方程联立得![]()
由韦达定理得:![]() ,即
,即![]()
类似可得![]()
①直线![]() 的斜率为
的斜率为![]()
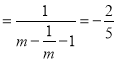 ,
,![]() 或
或![]() ,
,
当![]() 时,
时,![]() 方程为
方程为![]() ,
,![]()
此时直线![]() 的方程是
的方程是![]() 。同理,当
。同理,当![]() 时,直线
时,直线![]() 的方程也是
的方程也是![]() ,
,
综上所述:直线![]() 的方程是
的方程是![]()
②![]()
![]()
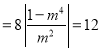
![]() 或
或![]()
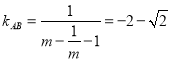 或
或![]()

练习册系列答案
相关题目