题目内容
16.已知函数f(x)=|x-2|+1,g(x)=loga(x+1)(a>0,且a≠1),若函数f(x)-g(x)有两个不相同的零点,则实数a的取值范围是( )| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (1,3) | D. | (3,+∞) |
分析 作出两个函数的图象,结合对数函数的单调性,利用数形结合即可得到结论.
解答 解:若函数f(x)-g(x)有两个不相同的零点,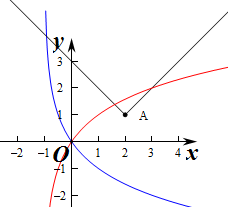
则等价为f(x)-g(x)=0有两个不相同的根,
即函数f(x)与g(x)有两个不相同的交点,
作出两个函数的图象如图:
则函数f(x)的最小值为1即A(2,1),
若0<a<1,则函数f(x)与g(x)有1个不相同的交点,不满足条件.
若a>1,要使函数f(x)与g(x)有两个不相同的交点,
则点A在g(x)的下方,
即g(2)>1,即g(2)=loga3>1,
解得1<a<3,
故实数a的取值范围是(1,3),
故选:C.
点评 本题主要考查函数交点个数的判断以及对数函数的单调性,利用数形结合是解决本题的关键.注意要对a进行讨论.

练习册系列答案
相关题目
11.若复数z满足(1-2i)z=2+i,则z的共轭复数是( )
| A. | -$\frac{3}{5}$i | B. | $\frac{3}{5}$i | C. | i | D. | -i |
1.阅读如图所示的程序框图,若输入m=6,则输出S等于( )
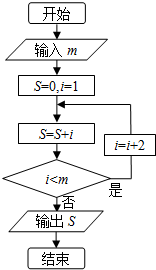

| A. | 4 | B. | 9 | C. | 16 | D. | 25 |
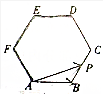 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$]. 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.