Question

16．如图，在四棱台ABCD-A₁B₁C₁D₁中，DD₁⊥底面ABCD，四边形ABCD为正方形，DD₁=AD=2，A₁B₁=1，C₁E∥平面ADD₁A₁．
（Ⅰ）证明：E为AB的中点；
（Ⅱ）求点E到平面ADC₁的距离．

Answer 1

分析 （Ⅰ）连接AD₁，则D₁C₁∥DC∥AB，证明四边形AEC₁D₁为平行四边形，即可证明：E为AB的中点；
（Ⅱ）利用等体积法求点E到平面ADC₁的距离．

解答 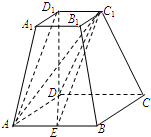（Ⅰ）证明：连接AD₁，则D₁C₁∥DC∥AB，
∴A、E、C₁、D₁四点共面，
∵C₁E∥平面ADD₁A₁，则C₁E∥AD₁，
∴AEC₁D₁为平行四边形，
∴AE=D₁C₁=1，∴E为AB的中点．（6分）
（Ⅱ）解：V${\;}_{{C}_{1}}$_-ADE=$\frac{1}{3}$DD₁×$\frac{1}{2}$AE×AD=$\frac{1}{3}$×2×$\frac{1}{2}$×2×1=$\frac{2}{3}$，DC₁=$\sqrt{5}$，
∵AD⊥DC，AD⊥DD₁，∴AD⊥平面DCC₁D₁，AD⊥DC₁．
设点E到平面ADC₁的距离为h，
则V${\;}_{{c}_{1}}$_-ADE=$\frac{2}{3}$=V_E-AD${\;}_{{c}_{1}}$=$\frac{1}{3}$h×$\frac{1}{2}$AD×DC₁=$\frac{\sqrt{5}}{3}$h，解得h=$\frac{2\sqrt{5}}{5}$．（13分）

点评 本题考查线面平行的性质，考查点E到平面ADC₁的距离，考查学生分析解决问题的能力，正确运用等体积转化是关键．