题目内容
(本小题满分14分)
在平面直角坐标系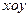 中,已知圆
中,已知圆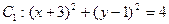 和圆
和圆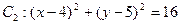 .
.
(1)若直线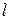 过点
过点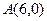 ,且被圆
,且被圆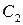
 截得的弦长为
截得的弦长为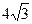 ,求直线
,求直线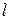 的方程;
的方程;
(2)在平面内是否存在一点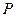 ,使得过点
,使得过点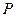 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线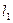 和
和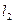 ,它们分别与圆
,它们分别与圆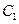 和圆
和圆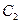 相交,且直线
相交,且直线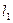 被圆
被圆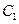 截得的弦长的
截得的弦长的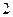 倍与直线
倍与直线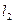 被圆
被圆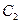 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的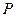 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
在平面直角坐标系
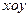 中,已知圆
中,已知圆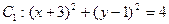 和圆
和圆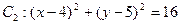 .
.(1)若直线
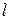 过点
过点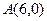 ,且被圆
,且被圆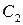
 截得的弦长为
截得的弦长为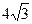 ,求直线
,求直线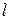 的方程;
的方程;(2)在平面内是否存在一点
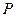 ,使得过点
,使得过点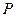 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线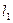 和
和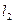 ,它们分别与圆
,它们分别与圆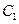 和圆
和圆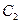 相交,且直线
相交,且直线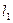 被圆
被圆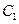 截得的弦长的
截得的弦长的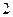 倍与直线
倍与直线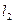 被圆
被圆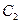 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的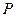 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由. |
(1)若直线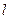 的斜率不存在,则过点
的斜率不存在,则过点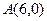 的直线为
的直线为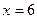 ,此时圆心
,此时圆心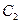
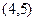 到直线
到直线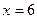 的距离为
的距离为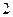 ,
,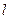 被圆
被圆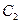 截得的弦长为
截得的弦长为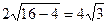 ,符合题意,所以直线
,符合题意,所以直线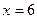 为所求. …………2分
为所求. …………2分
若直线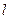 的斜率存在,可设直线
的斜率存在,可设直线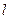 的方程为
的方程为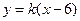 ,即
,即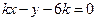 ,
,
所以圆心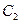 到直线
到直线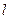 的距离
的距离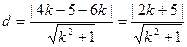 . …………3分
. …………3分
又直线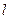 被圆
被圆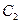 截得的弦长为
截得的弦长为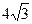 ,圆
,圆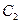 的半径为4,所以圆心
的半径为4,所以圆心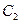 到直线
到直线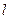 的距离应为
的距离应为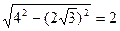 ,即有
,即有
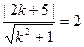 ,解得:
,解得: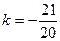 . …………4分
. …………4分
因此,所求直线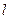 的方程为
的方程为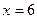 或
或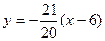 ,
,
即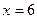 或
或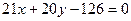 . …………5分
. …………5分
(2) 设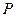 点坐标为
点坐标为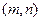 ,直线
,直线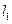 的斜率为
的斜率为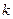 (不妨设
(不妨设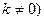 ,则
,则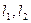 的方程分别为:
的方程分别为:
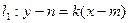 即
即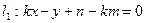 ,
,
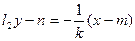 即
即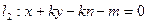 . …………6分
. …………6分
因为直线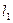 被圆
被圆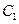 截得的弦长的
截得的弦长的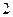 倍与直线
倍与直线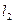 被圆
被圆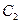 截得的弦长相等,又已知圆
截得的弦长相等,又已知圆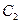 的半径是圆
的半径是圆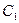 的半径的
的半径的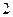 倍.由垂径定理得:圆心
倍.由垂径定理得:圆心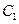 到直线
到直线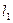 的距离的
的距离的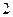 倍与
倍与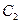 直线
直线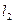 的距离相等.w .m
的距离相等.w .m  …………7分
…………7分
故有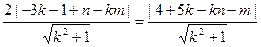 , …………10分
, …………10分
化简得: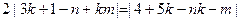 ,
,
即有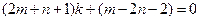 或
或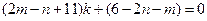 .
.
…………11分
由于关于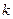 的方程有无穷多解,所以有
的方程有无穷多解,所以有
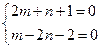 或
或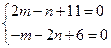 , …………12分
, …………12分
解之得:
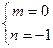 或
或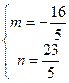 , …………13分
, …………13分
所以所有满足条件的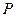 点坐标为
点坐标为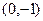 或
或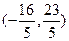 . …………14分
. …………14分
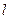 的斜率不存在,则过点
的斜率不存在,则过点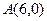 的直线为
的直线为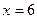 ,此时圆心
,此时圆心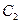
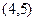 到直线
到直线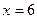 的距离为
的距离为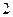 ,
,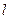 被圆
被圆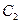 截得的弦长为
截得的弦长为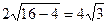 ,符合题意,所以直线
,符合题意,所以直线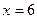 为所求. …………2分
为所求. …………2分若直线
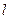 的斜率存在,可设直线
的斜率存在,可设直线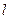 的方程为
的方程为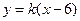 ,即
,即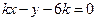 ,
,所以圆心
 到直线
到直线 的距离
的距离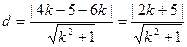 . …………3分
. …………3分又直线
 被圆
被圆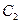 截得的弦长为
截得的弦长为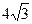 ,圆
,圆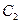 的半径为4,所以圆心
的半径为4,所以圆心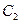 到直线
到直线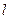 的距离应为
的距离应为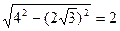 ,即有
,即有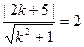 ,解得:
,解得: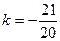 . …………4分
. …………4分因此,所求直线
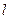 的方程为
的方程为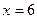 或
或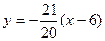 ,
,即
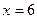 或
或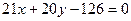 . …………5分
. …………5分(2) 设
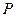 点坐标为
点坐标为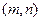 ,直线
,直线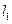 的斜率为
的斜率为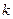 (不妨设
(不妨设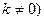 ,则
,则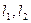 的方程分别为:
的方程分别为: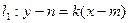 即
即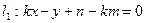 ,
,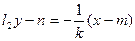 即
即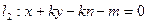 . …………6分
. …………6分因为直线
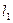 被圆
被圆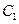 截得的弦长的
截得的弦长的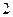 倍与直线
倍与直线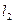 被圆
被圆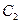 截得的弦长相等,又已知圆
截得的弦长相等,又已知圆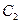 的半径是圆
的半径是圆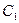 的半径的
的半径的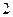 倍.由垂径定理得:圆心
倍.由垂径定理得:圆心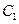 到直线
到直线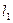 的距离的
的距离的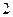 倍与
倍与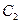 直线
直线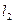 的距离相等.w .m
的距离相等.w .m  …………7分
…………7分故有
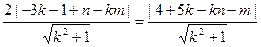 , …………10分
, …………10分化简得:
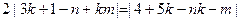 ,
,即有
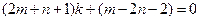 或
或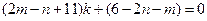 .
.…………11分
由于关于
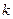 的方程有无穷多解,所以有
的方程有无穷多解,所以有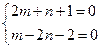 或
或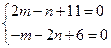 , …………12分
, …………12分解之得:
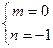 或
或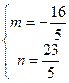 , …………13分
, …………13分所以所有满足条件的
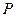 点坐标为
点坐标为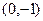 或
或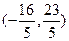 . …………14分
. …………14分略

练习册系列答案
相关题目
 ,
, ,则
,则 和
和 的位置关系是( )
的位置关系是( ) 圆过点
圆过点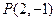 ,圆心在
,圆心在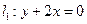 上,并与直线
上,并与直线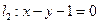 相切,求该圆的方程。
相切,求该圆的方程。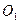 与⊙
与⊙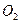 外
外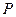 ,
,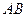 是两圆的外公切线,
是两圆的外公切线,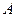 ,
,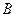 为切
为切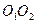 的延长线相交于点
的延长线相交于点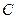 ,延长
,延长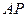
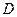 ,点
,点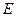 在
在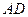 延长线上.
延长线上. 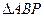 是直角三角形;
是直角三角形;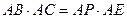 ,试判断
,试判断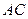 与
与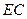 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.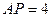 ,
,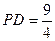 ,求
,求 的值.
的值.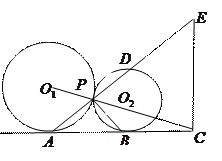
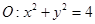 及点A(1,3),BC为
及点A(1,3),BC为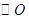 的任意一条直径,则
的任意一条直径,则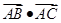 =( )
=( )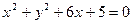 外切,同时与圆
外切,同时与圆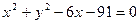 内切,则动圆圆心的轨迹方程是[
内切,则动圆圆心的轨迹方程是[