题目内容
已知圆C1:x2+y2-4x-2y-5=0,圆C2:x2+y2+2x-2y-14=0.
(1)试判断两圆的位置关系;
(2)直线ι过点(6,3)与圆C1相交于A,B两点,且|AB|=2
,求直线ι的方程.
(1)试判断两圆的位置关系;
(2)直线ι过点(6,3)与圆C1相交于A,B两点,且|AB|=2
| 6 |
(1)由于 圆C1:x2+y2-4x-2y-5=0,即 (x-2)2+(y-1)2=10,表示以C1(2,1)为圆心,
半径等于
的圆.
C2:x2+y2+2x-2y-14=0,即 (x+1)2+(y-1)2=16,表示以C2(-1,1)为圆心,半径等于4的圆.
由于两圆的圆心距等于
=3,大于半径之差而小于半径之和,故两个圆相交.
(2)直线ι过点(6,3)与圆C1相交于A,B两点,且|AB|=2
,当AB的斜率不存在时,直线ι的方程为x=6,
此时直线t与圆C1相离,不满足条件.
当AB的斜率不存在时,设直线ι的方程为y-3=k(x-6),即 kx-y+3-6k=0,
由弦长公式可得圆心到直线t的距离d=
=2,
再由点到直线的距离公式可得d=2=
,解得k=0,或 k=
.
故直线t的方程为 y=3或
x-y-5=0.
半径等于
| 10 |
C2:x2+y2+2x-2y-14=0,即 (x+1)2+(y-1)2=16,表示以C2(-1,1)为圆心,半径等于4的圆.
由于两圆的圆心距等于
| 32+0 |
(2)直线ι过点(6,3)与圆C1相交于A,B两点,且|AB|=2
| 6 |
此时直线t与圆C1相离,不满足条件.
当AB的斜率不存在时,设直线ι的方程为y-3=k(x-6),即 kx-y+3-6k=0,
由弦长公式可得圆心到直线t的距离d=
| 10-6 |
再由点到直线的距离公式可得d=2=
| |2k-1+3-6k| | ||
|
| 4 |
| 3 |
故直线t的方程为 y=3或
| 4 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
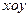 中,已知圆
中,已知圆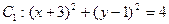 和圆
和圆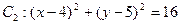 .
.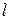 过点
过点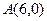 ,且被圆
,且被圆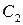
 截得的弦长为
截得的弦长为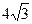 ,求直线
,求直线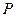 ,使得过点
,使得过点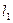 和
和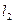 ,它们分别与圆
,它们分别与圆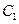 和圆
和圆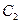 相交,且直线
相交,且直线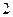 倍与直线
倍与直线
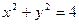 与圆
与圆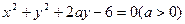 的公共弦长为
的公共弦长为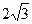 ,则a=________.
,则a=________.