题目内容
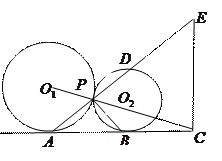
(本小题满分9分)如图,已知⊙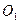 与⊙
与⊙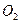 外
外
切于点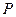 ,
,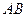 是两圆的外公切线,
是两圆的外公切线,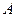 ,
,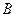 为切
为切
点,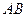 与
与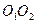 的延长线相交于点
的延长线相交于点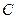 ,延长
,延长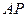
交⊙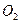 于 点
于 点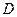 ,点
,点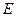 在
在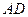 延长线上.
延长线上.
(1)求证: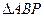 是直角三角形;
是直角三角形;
(2)若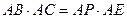 ,试判断
,试判断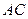 与
与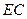 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.
(3)在(2)的条件下,若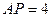 ,
,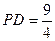 ,求
,求 的值.
的值.
 与⊙
与⊙ 外
外切于点
 ,
,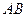 是两圆的外公切线,
是两圆的外公切线,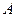 ,
,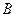 为切
为切点,
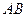 与
与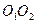 的延长线相交于点
的延长线相交于点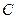 ,延长
,延长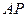
交⊙
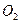 于 点
于 点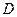 ,点
,点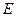 在
在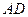 延长线上.
延长线上. (1)求证:
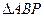 是直角三角形;
是直角三角形;(2)若
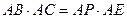 ,试判断
,试判断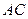 与
与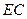 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.(3)在(2)的条件下,若
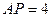 ,
,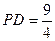 ,求
,求 的值.
的值.
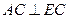 ,
,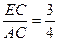
(1)证明:过点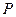 作两圆公切线
作两圆公切线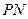 交
交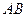 于
于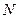 ,由切线长定理得
,由切线长定理得
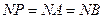 ,∴
,∴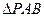 为直角三角形 ………………3分
为直角三角形 ………………3分
(2)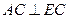
证明:∵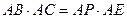 ,
,
∴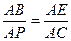 ,又
,又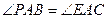 ,
,
∴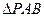 ∽
∽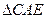
∴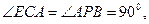 即
即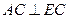 . ……………6分
. ……………6分
(3)由切割线定理,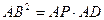 ,
,
∴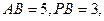
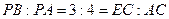
∴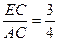 . ………………9分
. ………………9分
 作两圆公切线
作两圆公切线 交
交 于
于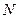 ,由切线长定理得
,由切线长定理得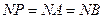 ,∴
,∴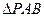 为直角三角形 ………………3分
为直角三角形 ………………3分(2)
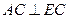
证明:∵
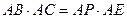 ,
,∴
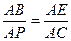 ,又
,又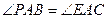 ,
, ∴
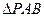 ∽
∽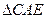
∴
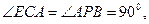 即
即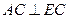 . ……………6分
. ……………6分(3)由切割线定理,
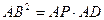 ,
,∴
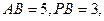
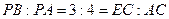
∴
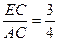 . ………………9分
. ………………9分
练习册系列答案
相关题目
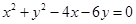 和圆:
和圆: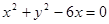 交于
交于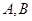 两点,则
两点,则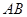 的垂直平分线的方程是( )
的垂直平分线的方程是( )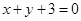 B
B 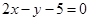 C
C 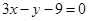 D
D 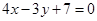
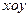 中,已知圆
中,已知圆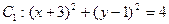 和圆
和圆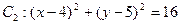 .
. 过点
过点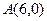 ,且被圆
,且被圆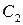
 截得的弦长为
截得的弦长为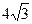 ,求直线
,求直线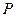 ,使得过点
,使得过点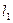 和
和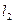 ,它们分别与圆
,它们分别与圆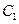 和圆
和圆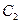 相交,且直线
相交,且直线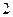 倍与直线
倍与直线
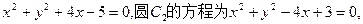 动圆C与圆C1、C2相外切。
动圆C与圆C1、C2相外切。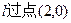 且与轨迹E交于P、Q两点。
且与轨迹E交于P、Q两点。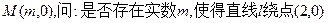 无论怎样转动,都有
无论怎样转动,都有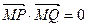 成立?若存在,求出实数m的值;若不存在,请说明理由;
成立?若存在,求出实数m的值;若不存在,请说明理由;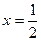 的垂线PA、QB,垂足分别为A、B,记
的垂线PA、QB,垂足分别为A、B,记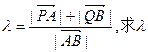 的取值范围。
的取值范围。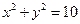 和
和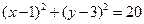 相交于
相交于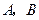 两点,则直线
两点,则直线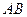 的方程是
的方程是 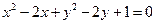 外一点
外一点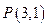 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为 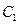 :
: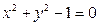 和圆
和圆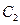 :
: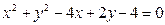 的位置关系是
的位置关系是