��Ŀ����
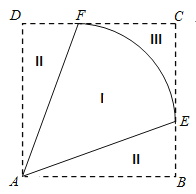
����Ŀ������һ��Ϊ����ʵ�������˶�һСʱ������ƻ���һ��ֱ��������ABC�Ŀյ�����һ��ռ�����ΪS�ľ���AMPN�������أ���ͼ����M��AC�ϣ���N��AB�ϣ���P����б��BC�ϣ���֪��ACB=60����|AC|=30�ף�|AM|=x�ף�x��[10��20]��
��1������x��ʾS������S��ȡֵ��Χ��
��2�����ھ���AMPN���⣨��Ӱ���֣����ϲ�ƺ����֪������AMPN��������ÿƽ�������Ϊ![]() ����ƺ��ÿƽ�������Ϊ
����ƺ��ÿƽ�������Ϊ![]() ��kΪ�����������������T����S�ĺ���ΪT=f��S�������ʣ����ѡȡ|AM|�ij�������ʹ�����T��ͣ�
��kΪ�����������������T����S�ĺ���ΪT=f��S�������ʣ����ѡȡ|AM|�ij�������ʹ�����T��ͣ�

���𰸡���1��![]() ��2��12��18��
��2��12��18��
��������
���⣨1���������⣬�����ɵã�����������ռ�������ֻ�����ͼ�о��ε�������ɣ��ٽ�Ͼ��ε�������㹫ʽ������ǵ�������ã�����ٸ��ݶ��κ��������ʵó��䷶Χ��
��2�����ڣ�1�����в���ʽ�����ǵ���������֮��Ϊ��ֵ�������û�������ʽ���������ֵ���Ӷ�������⣮
�⣺��1����Rt��PMC�У���Ȼ|MC|=30��x����PCM=60��
��|PM|=|MC|tan��PCM=![]() ��30��x������2��
��30��x������2��
����AMPN�����S=|PM||MC|=![]() x��30��x����x��[10��20]��4��
x��30��x����x��[10��20]��4��
����200![]() ��S��225
��S��225![]() ������6��
������6��
��2������AMPN�����������T1=37k![]() ��7��
��7��
����ABC�����Ϊ450![]() ������ƺ���T2=
������ƺ���T2=![]() S����8��
S����8��
�������T=T1+T2����T=25k��![]() +
+![]() ����200
����200![]() ��S��225
��S��225![]() ����10��
����10��
��T=25k��![]() +
+![]() ����200
����200![]() ��S��225
��S��225![]()
��![]() +
+![]() ��12
��12![]() ����11��
����11��
���ҽ���![]() =
=![]() ��S=216
��S=216![]() ʱ�Ⱥų�������12��
ʱ�Ⱥų�������12��
��ʱ![]() x��30��x��=216
x��30��x��=216![]() �����x=12��x=18��
�����x=12��x=18��
����ѡȡ|AM|�ij�Ϊ12��18��ʱ�����T��ͣ���14�֣�