题目内容
【题目】某地拟规划种植一批芍药，为了美观，将种植区域（区域I）设计成半径为1km的扇形
，中心角
（
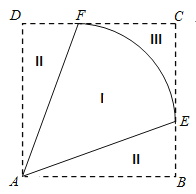
）.为方便观赏，增加收入，在种植区域外围规划观赏区（区域II）和休闲区（区域III），并将外围区域按如图所示的方案扩建成正方形
，其中点
，
分别在边
和
上．已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
（1）要使观赏区的年收入不低于5万元，求
的最大值；
（2）试问：当为多少时，年总收入最大？
【答案】（1）
（2）
【解析】
（1）由
，
，
，所以
与
全等.
可得
，根据面积公式，可求得观赏区的面积为
，要使得观赏区的年收入不低于5万元，则要求
，解不等式即可求出结果.
（2）由题意可得种植区的面积为
，正方形面积为
，设年总收入为
万元，则
，利用导数在函数单调性中的应用，即可求出结果.
（1）∵，，，所以与全等.
所以，观赏区的面积为
，要使得观赏区的年收入不低于5万元，则要求，即
，结合
可知
，则
的最大值为.
（2）种植区的面积为
，
正方形面积为
，
设年总收入为万元，则
，
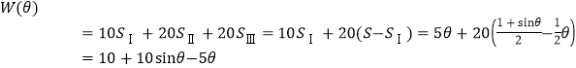其中，求导可得
.
当时，
，递增；当
时，
，递增.
所以当
时，取得最大值，此时年总收入最大.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
