题目内容
已知四棱锥P-ABCD的体积为V,AB∥CD,且AB:CD=2:3,点Q是PA的中点,则三棱锥Q-PBC的体积是( )
A.
| B.
| C.
| D.
|
由题意如图,因为AB:CD=2:3,底面梯形高相同,棱锥的高相同,所以P-ABC的体积为
V.
在棱锥P-ABC中,底面PBC的面积相同,点Q是PA的中点,Q到底面PBC的距离是A到底面PBC距离的一半,
所以三棱锥Q-PBC的体积是棱锥P-ABC体积的一半,
所以三棱锥Q-PBC的体积是:
×
V=
V.
故选A.

| 2 |
| 5 |
在棱锥P-ABC中,底面PBC的面积相同,点Q是PA的中点,Q到底面PBC的距离是A到底面PBC距离的一半,
所以三棱锥Q-PBC的体积是棱锥P-ABC体积的一半,
所以三棱锥Q-PBC的体积是:
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
故选A.


练习册系列答案
相关题目
 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知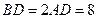 ,
, .
. (Ⅰ)设
(Ⅰ)设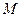 是
是 上的一点,证明:平面
上的一点,证明:平面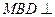 平面
平面 ;
;




