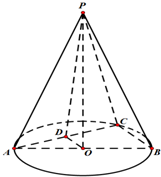
题目内容
在圆锥PO中,已知PO=2
,⊙O的直径AB=4,点C在底面圆周上,且∠CAB=30°,D为AC的中点.
(1)证明:AC⊥平面POD;
(2)求点O到面PAD的距离.
| 2 |
(1)证明:AC⊥平面POD;
(2)求点O到面PAD的距离.

(1)证明:∵PO⊥面ABC,且AC?面ABC∴AC⊥PO,
由于AB是直径,且点C在圆周上,∴AC⊥BC,
∵点O,D分别,AC的中点∴OD∥BC∴AC⊥OD,
又∵PO∩OD=O∴AC⊥面POD;
(2)由(1)知AC⊥面POD,又有AC?面PAC,
∴面PAC⊥面POD,
∵面PAC∩面POD=PD
作OH⊥PD,垂足为H,则有OH⊥面PAC
从而OH⊥面PAD,
在Rt△POD中,PO=2
,OD=
BC=
AB=1,
∴PD=3,
∴OH=
=
.

由于AB是直径,且点C在圆周上,∴AC⊥BC,
∵点O,D分别,AC的中点∴OD∥BC∴AC⊥OD,
又∵PO∩OD=O∴AC⊥面POD;
(2)由(1)知AC⊥面POD,又有AC?面PAC,
∴面PAC⊥面POD,
∵面PAC∩面POD=PD
作OH⊥PD,垂足为H,则有OH⊥面PAC
从而OH⊥面PAD,
在Rt△POD中,PO=2
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴PD=3,
∴OH=
| PO•OD |
| PD |
2
| ||
| 3 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则球的体积为________;
,则球的体积为________;