题目内容
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上.
的图像上.
(1)证明:当![]() 时,
时,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() 为数列
为数列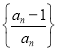 的前n项的积,若不等式
的前n项的积,若不等式![]() 对一切
对一切![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)证明见解析; (2)![]() (3)
(3)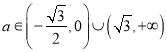
【解析】
(1)根据点在函数图像上,代入点坐标,化简后结合![]() 即可证明.
即可证明.
(2)根据(1)所得递推公式,递推作差后可得奇偶项分别为等差数列,根据![]() 和公差即可求得通项公式.
和公差即可求得通项公式.
(3)根据![]() 为数列
为数列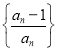 ,代入
,代入![]() 的通项公式求得
的通项公式求得![]() 的表达式,构造函数
的表达式,构造函数![]() ;代入
;代入![]() 的通项公式求得函数
的通项公式求得函数![]() ,根据恒成立求得
,根据恒成立求得![]() 即可.通过
即可.通过![]() 的单调性求得
的单调性求得![]() ,代入解不等即可得实数a的取值范围.
,代入解不等即可得实数a的取值范围.
(1)证明: 因为对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上
的图像上
所以![]() ,化简可得
,化简可得![]()
当![]() 时,
时, ![]()
两式相减可得![]()
即![]() (
(![]() )
)
原式得证.
(2)由(1)可知![]()
所以![]()
![]()
两式相减,可得![]()
所以数列![]() 的奇数项公差为4的等差数列,偶数项公差为4的等差数列.
的奇数项公差为4的等差数列,偶数项公差为4的等差数列.
由(1)可知![]()
则当![]() 时,
时, ![]() 求得
求得![]()
则当![]() 时,
时, ![]() ,即
,即![]() 求得
求得![]()
所以当![]() 为奇数时,
为奇数时, ![]()
所以当![]() 为偶数时,
为偶数时, ![]()
综上可知数列![]() 的通项公式为
的通项公式为![]()
(3)因为![]()
所以![]()
所以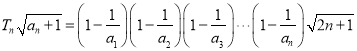
又因为![]()
所以![]() 对一切
对一切![]() 成立
成立
即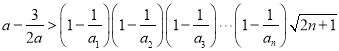 对一切
对一切![]() 成立
成立
只需满足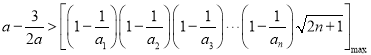 即可
即可
令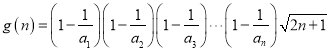
则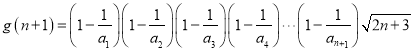
所以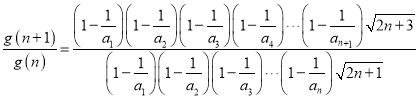

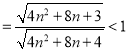
所以![]()
即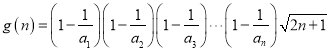 为单调递减数列
为单调递减数列
所以![]()
所以![]() 即可,化简可得
即可,化简可得
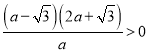
解不等式可得![]() ,或
,或![]()
故实数a的取值范围为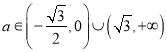

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目