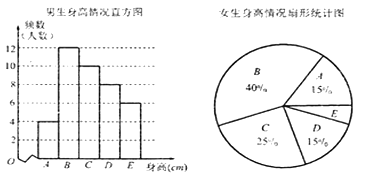
题目内容
【题目】为培养学生的阅读习惯，某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动. 活动后，为了解阅读情况，学校统计了甲、乙两组各10名学生的阅读量（单位：本），统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以a表示.
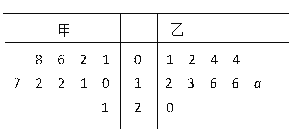
（Ⅰ）若甲组阅读量的平均值大于乙组阅读量的平均值，求图中a的所有可能取值；
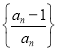
（Ⅱ）将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设
，现从所有的“阅读达人”里任取2人，求至少有1人来自甲组的概率；
（Ⅲ）记甲组阅读量的方差为
. 若在甲组中增加一个阅读量为10的学生，并记新得到的甲组阅读量的方差为
，试比较，的大小.（结论不要求证明）
（注：
，其中
为数据
的平均数）
【答案】（Ⅰ） 
或
. （Ⅱ） 
（Ⅲ） 
【解析】
（Ⅰ）分别求出甲组10名学生阅读量的平均值和乙组10名学生阅读量的平均值，由此能求出图中a的取值．
（Ⅱ）记事件“从所有的“阅读达人”里任取2人，至少有1人来自甲组”为M．甲组“阅读达人”有2人，在此分别记为A1，A2；乙组“阅读达人”有3人，在此分别记为B1，B2，B3．从所有的“阅读达人”里任取2人，利用列举法能求出从所有的‘阅读达人’里任取2人，至少有1人来自甲组的概率．
（Ⅲ）由茎叶图直接得
．
（Ⅰ）甲组10名学生阅读量的平均值为
，
乙组10名学生阅读量的平均值为
.
由题意，得
，即
.
故图中a的取值为或.
（Ⅱ）记事件“从所有的“阅读达人”里任取2人，至少有1人来自甲组”为M.
由图可知，甲组“阅读达人”有2人，在此分别记为
，
；乙组“阅读达人”有3人，在此分别记为
，
，
.
则从所有的“阅读达人”里任取2人，所有可能结果有10种， 即
，
，
，
，
，
，
，
，
，
.
而事件M的结果有7种，它们是，，，，，，
所以
.
即从所有的‘阅读达人’里任取2人，至少有1人来自甲组的概率为.
（Ⅲ）由茎叶图直接观察可得.
