题目内容
函数f(x)=log2x-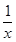 的零点所在的区间是________.
的零点所在的区间是________.
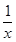 的零点所在的区间是________.
的零点所在的区间是________.(1,2)
利用零点存在定理求解.因为f(1)f(2)=(-1)· <0,所以由零点存在定理可知零点所在的区间是(1,2).
<0,所以由零点存在定理可知零点所在的区间是(1,2).
 <0,所以由零点存在定理可知零点所在的区间是(1,2).
<0,所以由零点存在定理可知零点所在的区间是(1,2).
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
题目内容
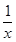 的零点所在的区间是________.
的零点所在的区间是________. <0,所以由零点存在定理可知零点所在的区间是(1,2).
<0,所以由零点存在定理可知零点所在的区间是(1,2).
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案