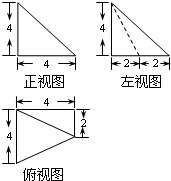
题目内容
5.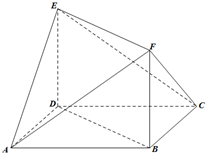 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.
(Ⅰ)求证:CF∥平面AED;
(Ⅱ)求直线AF与平面ECF所成角的正弦值;
(Ⅲ)在线段EC上是否存在点P,使得AP⊥平面CEF,若存在,求出$\frac{EP}{PC}$的值;若不存在,说明理由.
分析 (Ⅰ)根据线面平行的判定定理,可得:BC∥平面ADE,BF∥平面ADE,进而由面面平等的判定定理,可得平面BCF∥平面AED,进而根据面面平行的性质得到:CF∥平面AED;
(Ⅱ)建立空间直角坐标系O-xyz.求出直线AF的方向向量与平面ECF的法向量,代入向量夹角公式,可得直线AF与平面ECF所成角的正弦值;
(Ⅲ)设P(x,y,z),$\overrightarrow{EP}=λ\overrightarrow{EC}$,根据AP⊥平面CEF,则平面CEF法向量为$\overrightarrow{n}$满足:$\overrightarrow{AP}∥\overrightarrow{n}$,根据无满足条件的λ值,可得不存在这样的P点.
解答 证明:(Ⅰ)因为ABCD是菱形,
所以BC∥AD.
又BC?平面ADE,AD?平面ADE,
所以BC∥平面ADE..…(1分)
又因为BDEF是正方形,
所以BF∥DE.
因为BF?平面ADE,DE?平面ADE,
所以BF∥平面ADE…(3分)
因为BC?平面BCF,BF?平面BCF,BC∩BF=B,
所以平面BCF∥平面AED…(4分)
因为CF?平面BCF,
所以CF∥平面AED.….…..(5分)
解:(Ⅱ) 因为四边形ABCD为菱形,且∠BAD=60°,
所以△BCD为等边三角形…(6分)
取BD的中点O,
所以CO⊥BD,
取EF的中点G,连结OG,则OG∥DE
因为DE⊥平面ABCD,
所以OG⊥平面ABCD..…(7分)
如图建立空间直角坐标系O-xyz.
因为AB=2.
所以$O(0,0,0),A(0,-\sqrt{3},0),B(1,0,0),C(0,\sqrt{3},0),E(-1,0,2),F(1,0,2)$…(8分)
所以$\overrightarrow{AF}=(1,\sqrt{3},2)$,$\overrightarrow{FE}=(-2,0,0)$,$\overrightarrow{FC}=(-1,\sqrt{3},-2)$.
设平面CEF法向量为$\overrightarrow{n}$=(x,y,z),
则有$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{FE}=0\\ \overrightarrow{n}•\overrightarrow{FC}=0\end{array}\right.$
得 $\left\{{\begin{array}{l}{-2x=0}\\{-x+\sqrt{3}y-z=0}\end{array}}\right.$,
令y=1.则$\overrightarrow{n}=(0,1,\frac{\sqrt{3}}{2})$…(9分)
设AF与平面ECF所成的角为θ,则$sinθ=|cos<\overrightarrow{AF},\overrightarrow{n}>|=|\frac{\overrightarrow{AF}•\overrightarrow{n}}{|\overrightarrow{AF}||\overrightarrow{n}|}|=\frac{\sqrt{42}}{7}$,
所以直线AF与平面ECF所成角的正弦值为$\frac{{\sqrt{42}}}{7}$. ….…..(10分)
(Ⅲ)不存在…(11分)
$\overrightarrow{EC}=(1,\sqrt{3},-2)$,
设P(x,y,z),$\overrightarrow{EP}=λ\overrightarrow{EC}$,
由$\overrightarrow{AP}=\overrightarrow{AE}+\overrightarrow{EP}=\overrightarrow{AE}+λ\overrightarrow{EC}$,
得$\overrightarrow{AP}=(λ-1,\sqrt{3}λ+\sqrt{3},2-2λ)$…(12分)
因为平面CEF的法向量为 $\overrightarrow{n}=(0,1,\frac{\sqrt{3}}{2})$.
若AP⊥平面CEF,则$\overrightarrow{AP}∥\overrightarrow{n}$,即$\overrightarrow{AP}=μ\overrightarrow{n}$,..…(13分)
得$\left\{\begin{array}{l}λ-1=0\\ \sqrt{3}λ+\sqrt{3}=μ\\ 2-2λ=\frac{{\sqrt{3}}}{2}μ\end{array}\right.$
方程组无解,不符合题意.
综上,不存在λ使得AP⊥平面CEF.….…..(14分)
点评 本题考查的知识点是直线与平面平行的判定,直线与平面所成的角,向量法求线面夹角,难度中档.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案| A. | (-1,2) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
| A. | (2,-2) | B. | (-2,2) | C. | (-1,2) | D. | (2,-1) |
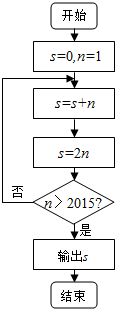
| A. | 210-1 | B. | 211-1 | C. | 21007-1 | D. | 21024-1 |