题目内容
20.由曲线y=x2,y=x围成的封闭图形的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 先根据题意画出区域,然后依据图形得到积分下限为0,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可
解答 解:由题意封闭图形如图, 得到积分上限为1,积分下限为0
得到积分上限为1,积分下限为0
直线y=x与曲线y=x2所围图形的面积S=∫01(x-x2)dx
而∫01(x-x2)dx=($\frac{1}{2}$x2-$\frac{1}{3}$x3)|${\;}_{0}^{1}$=$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$;
∴曲边梯形的面积是$\frac{1}{6}$;
故选:D.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,解题的关键就是求原函数

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
11.一个算法的程序框图如图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )


| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
8.已知抛物线y2=4x的准线与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的一条准线重合,则这条抛物线y2=4x与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的交点P到抛物线焦点的距离为( )
| A. | $\sqrt{21}$ | B. | 21 | C. | 6 | D. | 4 |
12.抛物线y=$\frac{1}{8}$x2上到焦点的距离等于10的点的坐标为( )
| A. | (-8,8) | B. | (8,8) | C. | (-8,-8)或(8,-8) | D. | (-8,8)或(8,8) |
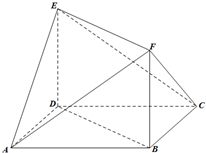 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,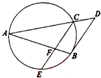 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.